マッチング

本稿では NetworkX の機能を利用して、グラフのマッチング問題各種を解く手順についてを記す。

極大マッチング

極大マッチングは関数呼び出し一発で求められる。

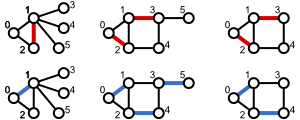
Wikipedia のイラストを参考にしてグラフを構築し、それぞれに対して関数 nx.maximal_matching を呼び出すコードを書いた。目的は、結果とイラストを比較して NetworkX の機能を確認することだ。

#!/usr/bin/env python
"""maximal_matching.py: demonstrate maximal_matching.
"""
import networkx as nx

def main():
    """The main function."""

    for edge_list in generate_edges():
        print(nx.maximal_matching(nx.Graph(edge_list)))

def generate_edges():
    """Generate edge lists to demonstrate maximal matching.

    Yields:
      Tuple of integer pairs.
    """

    # Fig. (a)
    yield (
        (0, 1), (0, 2),
        (1, 2),
        (3, 1),
        (4, 1),
        (5, 1))

    # Fig. (b)
    yield (
        (0, 1), (0, 2),
        (1, 2),
        (3, 1), (3, 4), (3, 5),
        (4, 2))

    # Fig. (c)
    yield (
        (0, 1), (0, 2),
        (1, 2),
        (3, 1), (3, 4),
        (4, 2))

if __name__ == '__main__':
    main()

実行結果は次の通り。当該記事の図とは異なるエッジセットが得られた。図の上の行がオリジナルで、下の行が本プログラムによる極大マッチングだ。確かにこのエッジセットもそれぞれのグラフの極大マッチングである

bash$ python maximal-matching.py
{(0, 1)}
{(0, 1), (2, 4), (3, 5)}
{(0, 1), (2, 4)}

最小極大マッチング

関数 min_maximal_matching が最小極大マッチングを求めるものなのだろうが、その実装は……。

最大マッチング

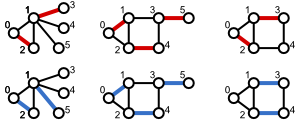
最大マッチングも関数呼び出し一発で求められる。こちらの例も Wikipedia から拝借して、結果を見比べてみよう。

コード例は左記の物とほぼ同様につき、差分のみを示す。関数 nx.max_weight_matching にはキーワード引数があるが、今回は未使用とする。

def main():
    """The main function."""

    for edge_list in generate_edges():
        print(nx.max_weight_matching(nx.Graph(edge_list)))

実行結果は次の通り。戻り値の型がノードとノードの辞書なのがマッチング感を演出しているように見受けられる。

bash$ python maximum_matching.py
{0: 2, 1: 5, 2: 0, 5: 1}
{0: 1, 1: 0, 2: 4, 3: 5, 4: 2, 5: 3}
{1: 3, 2: 4, 3: 1, 4: 2}

こちらも当該記事とは異なるエッジセットが得られた。図の上の行がオリジナルで、下の行が本プログラムによる最大マッチングだ。

Todo

あとは完全マッチング問題の解法を記述したい。