トポロジカルソート

本稿では NetworkX の提供する機能を利用して、有向グラフのトポロジカルソートを実行する方法について述べる。 NetworkX でトポロジカルソートを実現する関数は nx.topological_sort と nx.lexicographical_topological_sort である。まずは前者を見ていく。

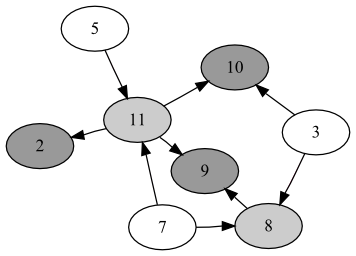
先にグラフ概形とサンプルコード全体を示す。

#!/usr/bin/env python
"""tsort.py: demonstrate NetworkX (topological_sort)
"""
import networkx as nx

def main():
    """The main function.

    Returns:
      None
    """

    G = setup_graph()
    print_sort(G)

def setup_graph():
    """Create a DAG to demonstrate topological_sort.

    Returns:
      (DiGraph): A DAG.
    """
    G = nx.DiGraph()

    # http://en.wikipedia.org/wiki/File:Directed_acyclic_graph.png
    G.add_edges_from((
        (7, 11),
        (5, 11),
        (11, 2),
        (11, 9),
        (3, 8),
        (8, 9),
        (3, 10),
        (7, 8),
        (11, 10)))

    #assert nx.is_directed_acyclic_graph(G)
    return G

def print_sort(G):
    """Execute topological_sort and print the result.

    Args:
      G (Graph): A DAG.

    Returns:
      None
    """
    print(list(nx.topological_sort(G)))

if __name__ == '__main__':
    main()

基本事項

グラフがトポロジカルソートを適用できる条件は、グラフが有向かつ閉路がないことが条件となる。つまり、グラフが DAG であることが条件である。 NetworkX では関数 nx.is_directed_acyclic_graph でグラフが DAG であるか否かをテストできる。そして実は DAG 性の判定はトポロジカルソートで実装されている。

そして、トポロジカルソートで少々注意を要するのは、一般的にはその結果が一意に決まらないということだろうか。サンプルコードは Wikipedia で DAG を論じるときによく参照されるグラフを拝借した。ページ中程に複数のソート結果が紹介されている。

関数 print_sort ではジェネレーター nx.topological_sort を呼び出し、実行結果を標準出力に書き出す。結果はこのようになった。見事に Wikipedia のどのソート結果とも異なる順列が得られた。

[7, 5, 11, 3, 8, 9, 10, 2]

しかし、これもまたトポロジカルソートの要件を満たしていることが容易に確認できる。ちなみに図のグラフのノードにわざわざ私が色を塗ったのは、色の明るいノードの順に得られるのでは、という予想だった。そしてそれは見事に外れたようだ。

辞書式トポロジカルソート

NetworkX におけるもう一つのトポロジカルソートの実装である。DFS 法を再帰的に呼び出す方式によるものだ。

試しに先のグラフに lexicographical 版を適用してみると、異なるソート結果が得られた。 Wikipedia の <smallest-numbered available vertex first> の結果と一致する。

>>> list(nx.lexicographical_topological_sort(G))
[3, 5, 7, 8, 11, 2, 9, 10]

ちなみに先に紹介した nx.topological_sort の実装はスキーナ本（邦訳：『アルゴリズム実装マニュアル』）から取ってきているらしい。