連結度

本稿では NetworkX にある、グラフの点および辺連結度に関係する機能を記す。

辺連結度と点連結度

辺連結度、点連結度は関数 nx.edge_connectivity と nx.node_connectivity でそれぞれ得られる。ここでは無向グラフいくつかに対して単に各連結度を計算した。

#!/usr/bin/env python
"""connectivity.py: demonstrate NetworkX edge_connectivity, etc.
"""
import networkx as nx

def main():
    """The main function.

    Returns:
        None.
    """

    for i, G in enumerate(generate_graphs()):
        print(f"G{i} is "
              f"{nx.node_connectivity(G)}-connected and "
              f"{nx.edge_connectivity(G)}-edge connected.")

def generate_graphs():
    """Generate graphs to demonstrate connectivities.

    Graphs are borrowed from:
    http://www.personal.kent.edu/~rmuhamma/GraphTheory/MyGraphTheory/connectivity.htm

    Yields:
      Graph instances.
    """

    # G0
    yield nx.MultiGraph((
        (0, 2), (2, 0),
        (1, 2),
        (3, 1)))
    # G1
    yield nx.Graph((
        (0, 1), (1, 2), (2, 0),
        (2, 3),
        (3, 4), (4, 6), (6, 3)))
    # G2
    yield nx.Graph((
        (0, 1), (1, 2), (2, 0),
        (2, 3), (3, 4), (4, 2)))
    # G3
    G = nx.cycle_graph(4)
    G.add_edge(3, 3)
    yield G

if __name__ == '__main__':
    main()

実行結果は次のようになる。

bash$ python connectivity.py
G0 is 1-connected and 1-edge connected.
G1 is 1-connected and 1-edge connected.
G2 is 1-connected and 2-edge connected.
G3 is 2-connected and 2-edge connected.

最小カットセット

関数 nx.minimum_edge_cut と nx.minimum_node_cut を利用すれば、グラフの辺、点に関する最小のカットセットを得られる。これらの関数のキーワード引数を用いて、カットに関する始点 s と終点 t を指定する。グラフを非連結にするようなカットを任意に一つ得たい場合には、これらの指定を省略することもできる。

次のコードは図のグラフに対して、両カット関数を色々な (s, t) の組み合わせで呼び出すものだ。

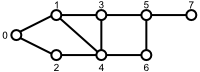
#!/usr/bin/env python
"""cutset.py: demonstrate NetworkX minimum_(edge|node)_cut.
"""
import networkx as nx

def main():
    """The main function.

    Returns:
        None.
    """

    # Set up a graph.
    # This graph is borrowed from the following article:
    # http://www.personal.kent.edu/~rmuhamma/GraphTheory/MyGraphTheory/connectivity.htm
    G = nx.Graph()
    G.add_path((0, 1, 3, 5, 7))
    G.add_path((0, 2, 4, 6, 5))
    G.add_edge(1, 4)
    G.add_edge(3, 4)
    print("G:", G.edges())

    st_pairs = ((0, 7), (0, 6), (1, 7),)
    for f in (nx.minimum_edge_cut, nx.minimum_node_cut):
        print(f"{f.__name__}: ")
        for s, t in st_pairs:
            print(f"(s, t) = ({s}, {t}): cutset = {f(G, s=s, t=t)}")

if __name__ == '__main__':
    main()

実行結果は次のようになる。よく見るとあまり面白くない。

bash$ python cutset.py
G: [(0, 1), (0, 2), (1, 3), (1, 4), (2, 4), (3, 4), (3, 5), (4, 6), (5, 6), (5, 7)]
minimum_edge_cut:
(s, t) = (0, 7): cutset = {(5, 7)}
(s, t) = (0, 6): cutset = {(5, 6), (4, 6)}
(s, t) = (1, 7): cutset = {(5, 7)}
minimum_node_cut:
(s, t) = (0, 7): cutset = {5}
(s, t) = (0, 6): cutset = {4, 5}
(s, t) = (1, 7): cutset = {5}