ネットワークフロー

本稿では NetworkX の提供する機能を利用して、各種ネットワークフロー問題を解決する方法について記す。

最大フロー

上下水道路、ガス管網、電線網、通信網、等々、ある種の「流れ」を表現するグラフが与えられているときに、その源流始点から終点までに流すことのできる水量なり電流なりの最大値、ここでは最大フローと呼ぶことにするが、この値を求める問題を解くための機能について記す。

各種ネットワークの水道管なり電線なりをグラフの辺として解釈するわけだが、その各辺に付随する容量を属性として定義するのが肝要だ。

お手軽な手法

NetworkX では最大フローを求める関数はズバリ nx.maximum_flow だ。まずはキーワード引数を全く指定せずに利用する例を示す。すなわち、グラフと始点と終点だけを指定するだけで最大フローを求める。

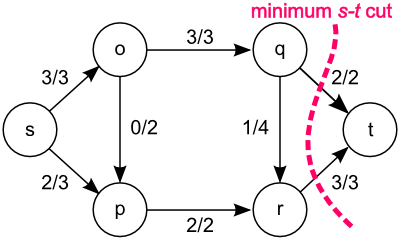
Wikipedia の説明文の図を拝借して、実行してみる。図の各辺のキャプションの / の右側の値が容量だから、グラフの構築コードは次のようになる。

#!/usr/bin/env python
"""maxflow.py: demonstrate NetworkX (maximum_flow).
"""
import networkx as nx

def main():
    """The main function.

    Returns:
        None.
    """

    # This graph is borrowed from:
    # http://en.wikipedia.org/wiki/Maximum_flow_problem
    G = nx.DiGraph()
    G.add_edges_from((('s', 'o', dict(capacity=3)),
                      ('s', 'p', dict(capacity=3)),
                      ('o', 'p', dict(capacity=2)),
                      ('o', 'q', dict(capacity=3)),
                      ('q', 'r', dict(capacity=4)),
                      ('q', 't', dict(capacity=2)),
                      ('p', 'r', dict(capacity=2)),
                      ('r', 't', dict(capacity=3)),))

    flow_value, flows = nx.maximum_flow(G, 's', 't')
    print(f'maximum flow: {flow_value}')

    caps = nx.get_edge_attributes(G, 'capacity')
    for u in nx.topological_sort(G):
        for v, flow in sorted(flows[u].items()):
            print(f'({u}, {v}): {flow}/{caps[(u, v)]}')

if __name__ == '__main__':
    main()

実行結果は次のようになる。最大フローが得られており、各辺の流量が Wikipedia の図の各辺のキャプションの / の左側の値と一致した。

bash$ python maxflow.py
maximum flow: 5
(s, o): 3/3
(s, p): 2/3
(o, p): 0/2
(o, q): 3/3
(q, r): 1/4
(q, t): 2/2
(p, r): 2/2
(r, t): 3/3

残余ネットワーク計算アルゴリズムを指定する手法

ここでは関数 nx.maximum_flow のキーワード引数 flow_func を明示的に指示する方法を記す。出来合いのアルゴリズムでは、以下の表に示すものが利用できる。グラフや容量の特性に合わせてアルゴリズムを選択するのだ：

関数	計算量	コメント
preflow_push	\(O(n^2 \sqrt{m})\)	デフォルトのアルゴリズム。
ford_fulkerson	\(O(nm^2)\)	レガシーな実装とのこと。
edmonds_karp	\(O(n m^2)\)	ford_fulkerson の「特殊版」の実装。
shortest_augmenting_path	\(O(\min(n^{2/3}, m^{1/2}) m)\)	最短増大路。

関数 nx.maximum_flow の実装を調べると、どうもこれらの関数のラッパーなのではないかという気がする。

インポートについては、例えば shortest_augmenting_path ならば次のように書けばよい。

from networkx.algorithms.flow import shortest_augmenting_path

最大フロー最小カット

先程の例と同じグラフを用いて、最小カットを求める手順を以下に示す。関数 nx.minimum_cut を利用するだけでよいのだが、最小カットが複数存在する場合でも、そのうちの一つを求めるようだ。

    # partition here is a tuple with the two sets of nodes that
    # define the minimum cut (S, T).
    cut_value, partition = nx.minimum_cut(G, 's', 't')
    S, T = partition

    print(f'cut value: {cut_value}')
    print(f'(S, T): ({S}, {T})')

    # Compute the cut set of edges that induce the minimum cut
    # as follows:
    cutset = set()
    for u, nbrs in ((n, G[n]) for n in S):
        cutset.update((u, v) for v in nbrs if v in T)
    print(f'cut set: {cutset}')

実行結果を次に示す。カットセットの構成本数が点 s, t に関する辺連結度 2 と一致している。

cut value: 5
(S, T): ({'o', 'r', 'p', 's', 'q'}, {'t'})
cut set: {('r', 't'), ('q', 't')}

当然ながら関数 nx.minimum_cut もキーワード引数 flow_func をサポートしているので、グラフの特性に適したアルゴリズムを指示するとよいだろう。

最小コストフロー

今まで見てきたのは、グラフの辺に容量という属性が付いた条件下の最大フロー算出問題だったが、ここではコストという概念を取り扱う。具体的には、フローを成立させるコストが最小になるようなものを求める。

輸送コストは辺に属性として指定する。属性値名はデフォルトでは weight だ。例によって各関数のキーワード引数 weight で明示的に指示できる。本稿では特に書き換えない。辺の容量の属性は引き続き capacity として指定する。なお、容量が未指定の辺も許される。グラフの構造によっては一部負の値の容量を持つものも許される。

例題はドキュメントを参照して欲しい。探すのが難しい。

最大フロー最小コスト

最大フロー最小コスト問題を考える。これは、各辺の容量とコストが与えられているときに、ある始点からある終点までの、可能な限り安くつく最大フローを求める問題だ。これを解くには、各属性を持つ辺の集合から有向グラフを適宜構築し、関数 nx.max_flow_min_cost と nx.cost_of_flow を用いて最大フローを得るという手順を踏むのがよさそうだ。

関数 nx.network_simplex

さらに、グラフの辺に輸送コストも付けたり、グラフの点に需要供給量を指定した状況でのフロー問題を解く機能について記す。

これには関数 nx.network_simplex を利用する。ただし必要に応じて、グラフの点に属性 demand を付加する。「流れ」が発生する点には負の値を、消費する点には正の値を指定する。

なお、最小コスト系の関数はすべて関数 nx.network_simplex で実装されている。