補間

本稿では補間曲線の構築方法である Lagrange 補間とスプライン補間について記す。 SciPy ではそれぞれ関数呼び出し一発で補間曲線が得られるので便利だ。

Lagrange 補間

普通は採用しない補間方式だが、関数 scipy.interpolate.lagrange を用いると Lagrange 補間多項式を得られる。単一の多項式で補間を表現するという性質上、多数の測定データに対して得られる補間多項式は次数が高くなり、数値計算に適さなくなる。次数が高いと、測定データから離れたパラメーターにおける補間関数の評価値が「暴れる」ので、補間としての質がそもそも問題外になる。SciPy のドキュメントでは、大体 20 個以上の点を寄越してくれるなと警告している。

コード的な手順は次のとおりとなる：

1. データ点列を array-like の形式で用意する。以下の説明ではそれぞれ x, y とする。

2. 関数 scipy.interpolate.lagrange に x, y を引数として呼び出す。戻り値が所望の補間多項式だ。

コード例を示す。Wikipedia の例から拝借した。

#!/usr/bin/env python
"""interp_lagrange.py: Demonstrate Lagrange interpolating.
"""
from scipy.interpolate import lagrange
import numpy as np

# pylint: disable=invalid-name

# x-coordinates of a set of datapoints
x = np.array([-1.5, -0.75, 0, 0.75, 1.5])

# y-coordinates of a set of datapoints
y = np.array([-14.1014, -0.931596, 0, 0.931596, 14.1014])

# Compute Lagrange interpolating polynomial.
f = lagrange(x, y)

print("Interpolating polynomial: \n", f)

私の環境での実行結果は次のとおり：

Interpolating polynomial:
        3            2
4.835 x - 2.22e-16 x - 1.477 x

任意のパラメーター t から補間値を計算する場合は、戻り値の多項式 f に対して f(t) と評価すればよい。

スプライン補間

スプライン補間はたいへんメジャーな補間方式であるので、ぜひ使えるようになりたい。ドローイングアプリケーション等で離散的な点列をなめらかに通過するような曲線を描く機能がよくある。こういうものにスプライン補間が利用できるのだ。

データが一次元の場合

金利表からスプライン補間を構築する例を挙げる。この表には 1, 3, 6, 12 ヶ月目の利息はあるが、その間の月次の利息が定義されていない。そこで、これらの利息を滑らかに接続するような補間曲線を構築すれば、任意の月次において支払額として妥当な値を算定できるようにできる。

コード的な手順は次のとおりとなる。

1. データ点列を array-like の形式で用意する。以下の説明ではそれぞれ x, y とする。

2. 関数 scipy.interpolate.splrep に x, y を引数として呼び出す。

3. 戻り値の tuple を適当な変数にセットする。以下の説明では tck とする。

この関数の戻り値はスプライン曲線を表現するための、三要素からなる tuple である。その要素とは

• ノットベクトル

• コントロールポイント列

• 曲線の次数

である。そう。スプラインというのは B-スプラインだったのだ。関数 splrep はキーワード引数で明示的に指定しない限り、使い勝手の良い 3 次のスプラインを返すようだ。

任意のパラメーター t から補間値を計算する場合は、戻り値のスプライン曲線の構成要素 tck を併用して、scipy.interpolate.splev(t, tck) のようにする。 splrep と splev はペアで覚えよう。

コード例を示す。金利データは某日に参照した資料 Japanese yen LIBOR interest rates in 2015 から拝借した。

#!/usr/bin/env python
"""interp_spline_interest.py: Demonstrate spline interpolation.
"""
from scipy.interpolate import splrep, splev
import numpy as np
import matplotlib.pyplot as plt

# pylint: disable=invalid-name

# Interest rates of Jan, Feb, Mar, Jun, Dec.
x = np.array([1, 2, 3, 6, 12])
y = np.array([0.080, 0.100, 0.112, 0.144, 0.266])

# Interpolate the rates.
tck = splrep(x, y)

# Print the spline curve.
np.set_printoptions(formatter={'float': '{:.3f}'.format})
print("knot vector:\n", tck[0])
print("control points:\n", tck[1])
print("degree:\n", tck[2])

# Evaluate interest rates for each month.
for i in range(1, 13):
    print(f"month[{i:02d}]: {float(splev(i, tck)):.3f}%")

# Plot the interest curve.
time = np.linspace(1, 12, 1000, endpoint=True)
rate = splev(time, tck)

plt.figure()
plt.plot(time, rate, color='deeppink')
plt.xlabel("Month")
plt.ylabel("Rate (%)")
plt.show()

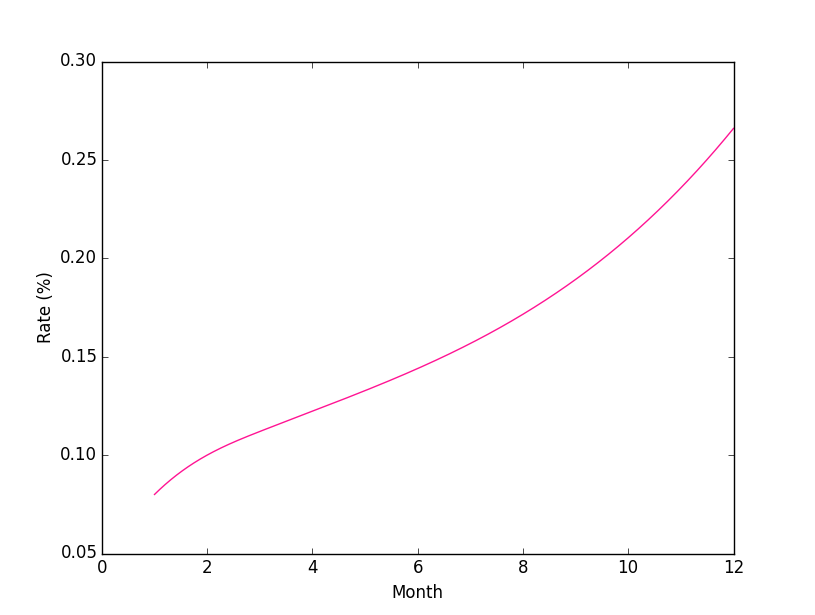
私の環境での実行結果は次のとおり。きちんと 1, 3, 6, 12 月の利率が入力データと一致しているし、補間された月次の利率も自然な印象を受ける値になっている。

knot vector:
 [1.000 1.000 1.000 1.000 3.000 12.000 12.000 12.000 12.000]
control points:
 [0.080 0.098 0.138 0.167 0.266 0.000 0.000 0.000 0.000]
degree (order - 1):
 3
month[01]: 0.080%
month[02]: 0.100%
month[03]: 0.112%
month[04]: 0.122%
month[05]: 0.133%
month[06]: 0.144%
month[07]: 0.157%
month[08]: 0.172%
month[09]: 0.189%
month[10]: 0.210%
month[11]: 0.236%
month[12]: 0.266%

プロットも見てみよう。

データが n 次元の場合

ドローイングツールでおなじみの「指定点列を滑らかに通過するスプライン曲線」を求める例を示す。ここでは n = 3 次元の点列の補間を試みる。デフォルトでは cubic なスプラインを計算するので、通過させたい点を 4 つ以上指定する必要がある。

コード的な手順は次のとおりとなる。

1. データ点列を array-like の形式で用意する。座標を縦ベクトルで表現して並べる感じだ。

2. 関数 scipy.interpolate.splprep にそれを引数として呼び出す。

3. 戻り値を tuple, float の形で受け取るべく適当な変数にセットする。以下の説明では tck および u とする。

   スプライン曲線のパラメーター列 u は、指定した点列を通過するときのパラメーターを保持する。

4. あとは先の例と同様だが、コントロールポイントの shape に注意すること。

コード例を示す。点列 \({(0, 0, 0)}\), \({(100, 0, 50)}\), \({(100, 100, 100)}\), \({(0, 100, 150)}\) を通過する cubic spline を作成するはずだ。

#!/usr/bin/env python
"""interp_spline_3d.py: Demonstrate spline interpolation.
"""
from scipy.interpolate import splprep, splev
import numpy as np
import matplotlib.pyplot as plt
# pylint: disable=unused-import
from mpl_toolkits.mplot3d import Axes3D

# pylint: disable=invalid-name, bad-whitespace

# Set 3D points.
points = np.array(
    [[0, 100, 100,   0],  # x
     [0,   0, 100, 100],  # y
     [0,  50, 100, 150]]) # z

# Interpolate points by a 3D curve.
tck, u = splprep(points)

# Print the spline curve.
np.set_printoptions(formatter={'float': '{:.3f}'.format}, precision=3)
print("knot vector:\n", tck[0])
print("control points:\n", np.array(tck[1]))
print("degree:\n", tck[2])
print("parameter values: \n", u)

# Evaluate the curve at each parameter i in u.
for i, xyz in zip(u, np.asarray(splev(u, tck)).T):
    print(f"f({i:.3f}) = {xyz}")

# Plot points and the curve.
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.scatter(xs=points[0], ys=points[1], zs=points[2],
           color='black', label='target points')
ax.plot(xs=tck[1][0], ys=tck[1][1], zs=tck[1][2],
        color='pink', label='control points')

params = np.linspace(u[0], u[-1], num=50, endpoint=True)
values = splev(params, tck)
ax.plot(xs=values[0], ys=values[1], zs=values[2],
        color='deeppink', label='cubic spline')

for pt in points.T:
    ptlabel = f"({pt[0]:d}, {pt[1]:d}, {pt[2]:d})"
    ax.text(pt[0], pt[1], pt[2], ptlabel, color='black')

ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.legend()
plt.show()

私の環境での実行結果は次のとおり。

knot vector:
 [0.000 0.000 0.000 0.000 1.000 1.000 1.000 1.000]
control points:
 [[0.000 150.000 150.000 0.000]
 [0.000 -116.667 216.667 100.000]
 [0.000 50.000 100.000 150.000]]
degree (order - 1):
 3
parameter values:
 [0.000 0.333 0.667 1.000]
f(0.000) = [0.000 0.000 0.000]
f(0.333) = [100.000 -0.000 50.000]
f(0.667) = [100.000 100.000 100.000]
f(1.000) = [0.000 100.000 150.000]

Matplotlib で立体的なプロットが実現できたので、出力結果を図像化しておいた。 空間曲線のプロット 参照。

薄ピンクの折れ線がコントロールポイントによる。この折れ線がスプライン曲線に対して convex hull property を満足していそうなことが目視で感じられる。例えば曲線の各端点における座標自身および接線方向が、対応する折れ線の各端点における座標自身および線分の方向と一致している。