応用テク ¶

本稿では LaTeX 表記の実現や 3D プロット等、比較的高度な Matplotlib の機能を利用する。

LaTeX 表現 ¶

Matplotlib のプロットに LaTeX 書式の画像化を埋め込む方法を説明する。

Matplotlib のすべてのテキスト API は LaTeX の数式を受け付けてくれる。文字列内の $ で囲まれた部分が LaTeX 表現と認識されるようだ。何も工夫しないでいると文字列がバックスラッシュの嵐になるので、 Python のコードで raw string 形式で数式を含む文字列を定義するのが吉だろう。

次のスクリプトは Matplotlib のサンプルコードを一部改変したものである。IPython を起動していれば、下記コードをクリップボードにコピーして、コンソールで %paste すれば結果が見られる。

#!/usr/bin/env python
"""tex.py: Demonstrate how to use TeX notation in Matplotlib.

You can obtain the original script file from:
From http://matplotlib.org/mpl_examples/statistics/histogram_demo_features.py
"""
from numpy.random import randn
from scipy.stats import norm
import matplotlib.pyplot as plt

# pylint: disable=invalid-name

NPDF_TEX = r'''
$\frac{1}{\sqrt{2 \pi}\sigma} \exp\left(-\frac{(x - \mu)^{2}}{2 \sigma ^{2}}\right)$
'''

# example data
MU = 100 # mean of distribution
SIGMA = 15 # standard deviation of distribution
x = MU + SIGMA * randn(10000)

NUM_BINS = 50
# the histogram of the data
n, bins, patches = plt.hist(
    x, NUM_BINS, density=True, facecolor='deeppink', label='random')

# add a 'best fit' line
y = norm.pdf(bins, MU, SIGMA)
plt.plot(bins, y, 'r--', label=NPDF_TEX)
plt.xlabel('Smarts')
plt.ylabel('Probability')
plt.title(rf'Histogram of IQ: $\mu={MU}$, $\sigma={SIGMA}$')
plt.legend(loc='upper left', shadow=True)

# Tweak spacing to prevent clipping of ylabel
plt.subplots_adjust(left=0.15)
plt.show()

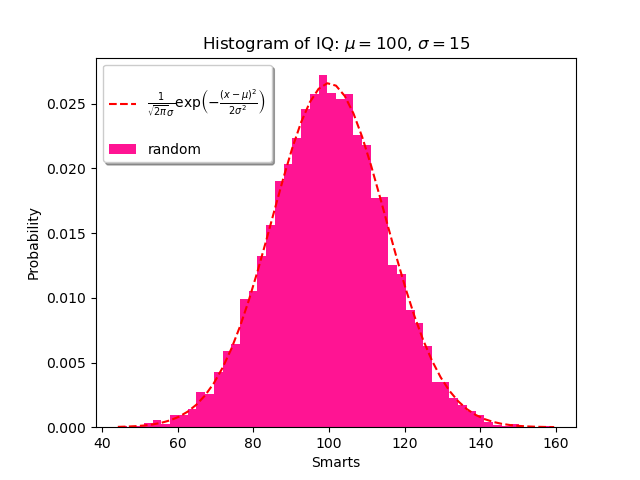
実行結果は次のような画像の表示となる（良いグラフとはとても言えない）。乱数を利用しているヒストグラム部分は毎回絵が変わる。図の凡例およびキャプション後半に注意して欲しい。ギリシア文字を含む数式が見える。

凡例内の数式は関数 plt.plot のキーワード引数 label の値の LaTeX と対応している。
図のキャプションのギリシア文字は、関数 plt.title に渡す値の LaTeX と対応している。

三次元プロット ¶

曲面を描画することもあるのでプロットという表現が微妙なのだが、とにかく空間的に三次元のデータを図にすることができる。

パッケージ matplotlib と同じ階層に mpl_toolkits という別のパッケージがある。ここにある機能を利用すると、三次元プロットをウィンドウに描画することができる。これはマウス操作によるビューのズームおよび回転を実現している優れものである。

ノート補間で示した例を再掲する。

#!/usr/bin/env python
"""interp_spline_3d.py: Demonstrate spline interpolation.
"""
from scipy.interpolate import splprep, splev
import numpy as np
import matplotlib.pyplot as plt
# pylint: disable=unused-import
from mpl_toolkits.mplot3d import Axes3D

# pylint: disable=invalid-name, bad-whitespace

# Set 3D points.
points = np.array(
    [[0, 100, 100,   0],  # x
     [0,   0, 100, 100],  # y
     [0,  50, 100, 150]]) # z

# Interpolate points by a 3D curve.
tck, u = splprep(points)

# Print the spline curve.
np.set_printoptions(formatter={'float': '{:.3f}'.format}, precision=3)
print("knot vector:\n", tck[0])
print("control points:\n", np.array(tck[1]))
print("degree:\n", tck[2])
print("parameter values: \n", u)

# Evaluate the curve at each parameter i in u.
for i, xyz in zip(u, np.asarray(splev(u, tck)).T):
    print(f"f({i:.3f}) = {xyz}")

# Plot points and the curve.
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.scatter(xs=points[0], ys=points[1], zs=points[2],
           color='black', label='target points')
ax.plot(xs=tck[1][0], ys=tck[1][1], zs=tck[1][2],
        color='pink', label='control points')

params = np.linspace(u[0], u[-1], num=50, endpoint=True)
values = splev(params, tck)
ax.plot(xs=values[0], ys=values[1], zs=values[2],
        color='deeppink', label='cubic spline')

for pt in points.T:
    ptlabel = f"({pt[0]:d}, {pt[1]:d}, {pt[2]:d})"
    ax.text(pt[0], pt[1], pt[2], ptlabel, color='black')

ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.legend()
plt.show()

Matplotlib 関連の処理の説明を補足する（曲線データに関しての説明は先のページを参照）。

関数 gca の呼び出しでカレントの Axes を指定する際に、キーワード引数 projection を 3d とすることで 3D プロット専用の Axes を生成し、同時にカレントにセットする。
- このメソッド呼び出しが成功するには Axes3D のインポートが必要。Pylint に警告されても必要。
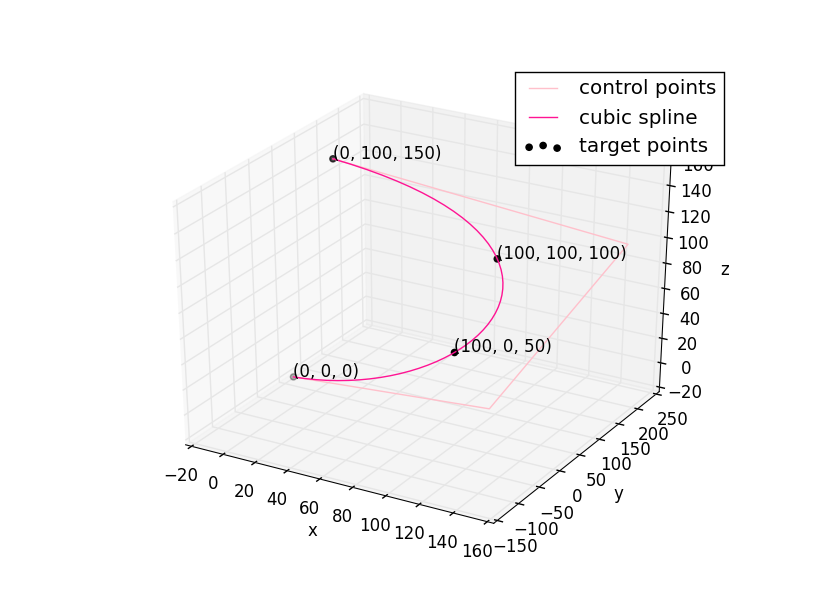
メソッド cur_axes.scatter と cur_axes.plot を用いて次の形状をプロットする。
1. 入力データである通過点 (black)
2. SciPy で計算した、出力データである三次元スプライン曲線の制御点列 (pink)
3. 出力データである三次元スプライン曲線 (deeppink)
メソッド cur_axes.text で通過点のプロットにその座標をテキストとして表示する。
各種メソッドでラベルや凡例を図に添える。

応用テク¶

LaTeX 表現¶

三次元プロット¶

応用テク ¶

LaTeX 表現 ¶

三次元プロット ¶