第 3 章 多様体の定義(前編)¶
\(\require{amscd}\)
多様体はユークリッド空間内になくてもよさそうだという考えが微分可能多様体の概念が生まれるきっかけとなった。
3.1 微分可能多様体の定義¶
定義 3.1.1: \(n\) 次元 (微分可能)多様体
以降、単に「多様体」と書くときは「微分可能多様体」を意味するものとする。
\(C^\infty\) 級多様体の定義は、前章までに見てきた位相多様体や \(C^r\) 級多様体の上位?概念のように捉えられる。
本書では下の図式の右下二つの多様体を主に扱うことになる。
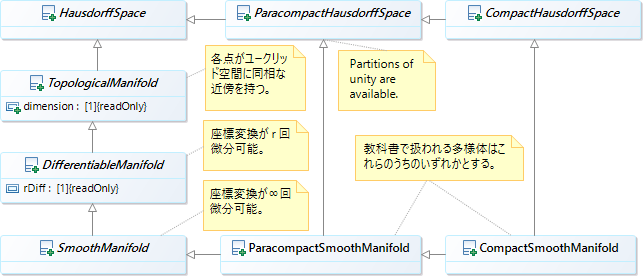
本書が対象とする多様体¶
例 3.1.5: 2 次曲面
\[Q = \Set{(X_1, \dotsc, X_n) \in \RR^n \Sth \sum_{i = 1}^n \lambda_i X_i^2 = b\quad(\ne 0)}\]座標近傍系を定義することで、曲面が多様体であることを示す。
\({U_i^+ \coloneqq Q \cap \set{X_i > 0}, \varphi_i^+(X_1, \dotsc, X_n) = (X_1, \dotsc, \widehat{(i)}, \dotsc, X_n)}\) などと置く(ハットの部分は除去を意味する)。
開集合 \(U_i^\pm\) をすべて合併させると曲面全体を覆う。
写像 \(\fn{\varphi_i^\pm}{Q}\RR^{n - 1}\) はちょっとした計算により同相写像であることを示せる。
座標変換 \({\varphi_i^\sigma \circ (\varphi_j^\tau)\inv}\) が \(C^\infty\) 級であることも同様にして示せる。
例 3.1.6: 多様体の直積、直和はどちらも多様体
次のようにして位相が定まる:
直積の位相: \(U_1 \times U_2\) の任意個の和集合を開集合とする。
直和の位相: \(U_1 \sqcup U_2\) を開集合とする。
3.2 商空間(基礎)¶
確認: 商空間 \(X/\sim\) の位相の入れ方、誘導される写像。
例 3.2.1: \(n + 1\) 次元空間内の「球面」
\(S^n\) の 対蹠点 を同一視することで構成される射影空間 \(\RR P^n\) は多様体となる。
前半は「球面」が多様体であることを示す。
局所座標系 \(\set{(U_i^\pm, \varphi_i^\pm)}\) を次のように定義する:
\begin{align*} U_i^\pm & = \set{(x_0, \dotsc, x_n) \in S^n \sth \pm x_i > 0},\\ \varphi_i^\pm (x_0, \dotsc, x_n) & = \left( \frac{x_0}{x_i}, \dotsc, \widehat{(i)}, \dotsc, \frac{x_n}{x_i} \right) \end{align*}各 \(\varphi_i^\pm\) は対応する \(U_i^\pm\) 上で連続となり、逆写像もまた連続となる。これで同相写像であることは言える。
次に座標変換 \({\varphi_j^+(U_i^- \cap U_j^+) \longto \varphi_i^-(U_i^- \cap U_j^+)}\) などを計算して、これらがすべて滑らかであることを示す。
後半は射影空間が多様体であることを示す。
射影 \(\fnm{p}{S^n}{\RR P^n}{[x]}\set{x, -x}\) は同値類への写像となる。
局所座標系 \(\set{(V_i, \varphi_i)}\) を次のように定義する:
\begin{align*} V_i & = \set{[\bm{x}] \in \RR P^n \sth x_i \ne 0},\\ \varphi_i([\bm{x}]) &= \varphi_i^\pm(\bm{x}) \end{align*}このとき、写像 \(\varphi_i\) は well-defined かつ連続写像かつ逆写像が存在する。
逆写像 \(\varphi_i\inv\) は \({p \circ (\varphi_i^+)\inv = p \circ (\varphi_i^-)\inv}\) となって連続である。図を入れたい。
次に座標変換が滑らかであることを示す。これは \({\varphi_i \circ \varphi_j\inv}\) が「球面」のときと同じ式で定義されることから言える。
射影空間がハウスドルフであることを示す。「球面」がハウスドルフであることと \({[\bm{x^1}] \ne [\bm{x^2}] \implies \bm{x^1} \ne \pm \bm{x^2}}\) であることから地道に示す。
3.3 変換群¶
用語確認
位相空間の変換群:同相写像の場合、写像の合成と逆写像をとる操作で閉じている。
作用 する
定理 3.3.1: 位相空間の有限変換群による商空間はハウスドルフ空間となる。
元の位相空間自身はハウスドルフ空間である必要はない。
\({[x] \ne [y]}\) となる \({x, y \in X}\) をとる。変換群を \({F = \set{f_i}_{i = 1, \dots, n},\ f_1 = \id}\) とおく。
まず各 \(i\) に対して次が成り立つ開集合 \({U_i, V_i \subset X}\) があることに注意:
\[x \in U_i, f_i(y) \in V_i, U_i \cap V_i = \varnothing.\]これは背理法で示せるのだが、簡単なためか紙幅の都合上か本書では触れていない。
次に \({\displaystyle U = \bigcap_{i = 1}^n U_i,\ V = \bigcap_{i = 1}^n f_i\inv(V_i)}\) とおく。このとき次が成り立つ:
\({x \in U},\ {y \in V.}\)
\({f_i(U) \cap f_j(V) = \varnothing} \text{ for } {i, j = 1, \dots, n.}\)
二番目の等式は \({f_i\inv \circ f_j = f_k}\) と表すと、次のようにしてわかる:
\[\begin{split}\begin{align*} f_i\inv(f_i(U) \cap f_j(V)) &= U \cap (f_i\inv \circ f_j)(V)\\ &= U \cap f_k(V)\\ &\subset U_k \cap V_k = \varnothing. \end{align*}\end{split}\]このとき射影 \(\fn{p}{X}X/F\) に対して \({[x] \in p(U),\ [y] \in p(V)}\) である。
例えば \({\displaystyle p\inv(p(U)) = \bigcup_{i = 1}^n f_i(U)}\) であるから(もっと丁寧に説明したい) \({[x] \in p(U)}\) と言える。 \({[y] \in p(V)}\) についても同じ。
最後に \({p\inv(p(U) \cap p(V)) = \varnothing}\) を示して、 \(P(U)\) と \(P(V)\) が先の同値類を分離する開集合であることを示す。射影が連続写像なのでこういう等式変形となる:
\[\begin{split}\begin{align*} p\inv(p(U) \cap p(V)) &= p\inv(p(U)) \cap p\inv(p(V))\\ &= \left(\bigcup_{i = 1}^n f_i(U)\right) \cap \left(\bigcup_{i = 1}^n f_i(V)\right)\\ &= \varnothing \quad(\because f_i(U) \cap f_j(V).) \end{align*}\end{split}\]
この節は例題と問題が多い。どれも大切。ハウスドルフ空間であることを示すために、二点が「関数で分離される」ことを示す必要がある場合のコツなど。
例題 3.3.2: 平面から原点を取り除いた空間において、水平な(半)直線に属する点同士を同値類とする商空間は多様体とはならない。
考察対象の空間
\({Z = \RR^2 \minuszero}\),
\({Y = Z / \sim}\)
考察する写像
\(\fnm{p}{Z}{\RR}{(x, y)}y\)
\(\fnm{\underline{p}}{Y}{\RR}{[x, y]}y\)
\(\fnm{f^\pm}{\RR}{Z}{y}(\pm 1, y)\)
\(\fn{p_Y}{Z}Y\) (射影)
合成写像 \({p_Y \circ f_\pm}\) を考える。\({Y_\pm \coloneqq (p_Y \circ f_\pm)(\RR)}\) とおくと、\(\underline{p}\) との絡みで \(Y_\pm\) と実数全体が同相であることを示せる。商空間の任意の点について、それを含む開近傍が \(Y_+\) か \(Y_-\) にあると結論できる。
\begin{align*} \begin{CD} \RR @>{f^\pm}>> Z @>{p_Y}>> Y_\pm \subset Y\\ @. @V{p}VV @V{\underline{p}}VV\\ @. \RR @. \RR \end{CD} \end{align*}商空間はハウスドルフではない。数直線の正の部分と負の部分が(見てくれに反して)分離できない。
問題 3.3.3: 平面から原点を取り除いた空間において、直角双曲線と座標軸に沿う半直線四本で埋め尽くされる商空間(双曲線や座標軸の部品を点とみなす)は多様体とはならない。
\begin{CD} \RR @>{g_\pm,\ h_\pm}>> Z @>{p_X}>> X_\pm^g, X_\pm^h = X\\ @. @V{p}VV @V{\underline{p}}VV\\ @. \RR @. \RR \end{CD}商空間の任意の点に対して、それを含む開近傍が存在して、ある開区間と同相とはなるものの、商空間はハウスドルフではない。
この問題は、考える写像がけっこうあるので図式をスケッチしながら解く。
問題 3.3.4: 平面から原点を除いた部分を図形で埋め尽くして同値類のなす商空間が多様体にならないパターンの問題。
行列 \({A = \displaystyle \begin{pmatrix} a & 0 \\ 0 & \dfrac{1}{a} \end{pmatrix}\ (a > 1)}\) をとり、元の空間における同値関係を \({z_1 \sim z_2 \iff \exists n \in \ZZ: A^n z_1 = z_2}\) で定義する。
同値関係であることを確認するのは簡単なので紙幅を割いていない。
対象となる空間は \({Z = \RR^2 \minuszero,\ S = Z / \sim}\)
前半は、\(S\) の各点に \(\RR^2\) と同相な近傍があることを示す。
点 \({(x, y) \in Z}\) に対して
\({x \ne 0}\) ならば開区間 \({\displaystyle I = \left(\frac{1}{\sqrt{a}}x, \sqrt{a}x \right)}\) を導入して \({I \times \RR}\) を、
\({y \ne 0}\) ならば開区間 \({\displaystyle I = \left(\frac{1}{\sqrt{a}}y, \sqrt{a}y \right)}\) を導入して \({\RR \times I}\) をそれぞれ考える。
このような直積を対応する点を含む \(Z\) の開集合とする。以下、しばらくは \({x \ne 0}\) で話をすすめる。
写像 \(\fn{p_s}{Z}S\) を射影とする。
写像 \(\fn{i}{I \times \RR}Z\) を包含写像とする。
写像 \(\fn{s: W }{= (p_s \circ i)(I \times \RR) } I \times \RR\) を代表元を取る写像とする。
\begin{CD} I \times \RR @>{i}>> Z @>{p_s}>> W \subset S @>{s}>> I \times \RR \end{CD}次の点を確認する必要がある:
\(s\) は well-defined である
これは \({I \times \RR}\) と各同値類の交点が高々一点であることから成り立つ。どう確かめるのがいいのか。
\(s\) は連続写像である
開集合 \({U \subset I \times \RR}\) をとると \(s\inv(U)\) が開集合であればよい。\({p\inv\circ s\inv(U)}\) が開集合であることを示すのがよい。\({\displaystyle \bigcup_{n \in \ZZ}A^n(U)}\) の代表元がどうなるかを考える。
\(s\) は同相写像である
すなわち \({W \cong I \times \RR}\) を示す。 \({s \circ (p_s \circ i) = \id_{I \times \RR}}\) と \({(p_s \circ i) \circ s = \id_W}\) であると言う。
\({W \cong I \times \RR \implies I \times \RR \cong \RR^2\ ([x] \in W)}\) を示す。
後半のハウスドルフではないことの証明は、\({[1, 0]}\) の近傍と \({[0, 1]}\) の近傍がどうしても共通部分があることを示すことにする。
例題 3.3.5: \({\RR/\ZZ \cong S^1}\) は多様体になる。
同値関係 \({x_1 \sim x_2 \iff x_1 - x_2 \in \ZZ}\) で商空間 \({\RR/\sim}\) を定義する。
射影を \(p\) とする。
ある閉集合の像 \({p(\set{0 \le x \le 1})}\) が空間全体となるゆえ、商空間はコンパクトであるといえる。
座標近傍系を次のように構成する。
同値類 \([x]\) に対して開区間 \({I_x \coloneqq (x - 1/4, x + 1/4) \subset \RR}\) を定義する。
同値類からその代表元を \(I_x\) の中にあるように取る(?)写像を \(s_x\) を定義する。
\(s_x\) は連続となる。なぜなら開集合 \({U \subset I_x}\) に対して \({ \displaystyle p\inv(s_x\inv(U)) = \bigcup_{n \in \ZZ}\set{x + n \sth x \in U} }\) は開集合だから。
\(s_x\) は同相となる。なぜなら \({(p|I_x) \circ s_x = \id,\quad s_x \circ (p|I_x) = \id}\) であるから。
\(\set{(p(I_x), s_x)}_{x \in \RR}\) が構成できた。
これがハウスドルフであることを直接示すのは面倒。
円周 \(S^1\) と同相となることを示せる。
実数から円周への写像 \({h: x \longmapsto (\cos 2\pi x, \sin 2 \pi x)}\) を定義する。
誘導される写像 \({\underline{h} = h \circ p\inv}\) が定義でき、これが全射であるだけでなく、単射であることを示せば、同相であると結論できる。
例題 3.3.6: \({\RR P^n = S^n / \set{\pm 1} = (\RR^{n + 1} \minuszero) / \RR^\times}\)
次のような写像 \(\fn{f}{\RR^{n + 1} \minuszero}\RR\) をまず定義し、これが well-defined であることを確認する。
\begin{align*} f(\bm{x_2}) = \frac{\abs{\bm{x_1} \cdot \bm{x_2}}}{\norm{\bm{x_1}} \norm{\bm{x_2}}}. \end{align*}次に誘導される写像 \(\underline{f}\) が連続であることを示し、コーシー・シュワルツの不等式の等式成立条件などからハウスドルフであることを示す。
多様体であることを示すために、局所座標系 \(\set{(V_i, \varphi_i)}\) を定義する。
\begin{align*} V_i & = \set{[\bm{x}] \in \RR^{n + 1} \zeroset \sth x_i \ne 0},\\ \varphi_i([\bm{x}]) &= \left( \frac{x_0}{x_i}, \dotsc, \widehat{(i)}, \dotsc, \frac{x_n}{x_i} \right) \end{align*}TODO: ここに包含写像を説明する可換図式みたいなものを挿れたい。
座標変換が滑らかであることを示す。
射影空間では超平面とそれに含まれない直線とは必ず一点で交わる。
問題 3.3.7: \(\CC P^n\)
\(\CC P^n\) はハウスドルフである
例題 3.3.6 と同様の実数値関数 \(\fn{f}{(\CC^{n + 1})^\times}\RR\) を定義する。
同様の理由により、\(f\) は \(\bm z_1\) の取り方によらず値が確定する。また、誘導される関数 \({\fn{\underline f}{(\CC^{n + 1})^\times/\sim = \CC P^n} \RR}\) も同様の理由により連続関数として確定する。
再びコーシー・シュワルツの不等式より \({\underline f \le 1.}\) 等号成立条件は \(\exists \lambda \in \CC^\times \text{ s.t. } {\bm z_1 = \lambda \bm z_2.}\) これは \({[\bm z_1] = [\bm z_2]}\) を意味する。ゆえに \({[\bm z_1] \ne [\bm z_2] \iff \underline f([\bm z_1]) \ne \underline f([\bm z_2]).}\)
相異なる二点を連続関数で分離されることを示せたので、この空間はハウスドルフである。
\(\CC P^n\) は実 \(2n\) 次元多様体である
座標近傍系を次のように定義する:
\[\begin{split}\begin{align*} V_i &= \set{[\bm z] \in (\CC^{n + 1})^\times/\sim \sth z_i \ne 0},\\ \varphi_i([\bm z]) &= \left(\frac{x_0}{x_i}, \dotsc, \widehat{(i)}, \dotsc, \frac{x_n}{x_i}\right). \end{align*}\end{split}\]次の性質がある:
各座標 \(\varphi_i\) は \(V_i\) 上の連続関数である(分母はゼロでないから)。
各座標 \(\varphi_i\) は同相写像である。
これを示すには \(\fn{\iota_i}{\CC^n}\CC^{n + 1}\) を次のように定め、これまでの問題にあるように射影 \(p\) と合成して \({\varphi_i \circ (p \circ \iota_i) = \id_{\CC^n}}\) かつ \({(p \circ \iota_i) \circ \varphi_i = \id_{V_i}}\) であるから同相となると言う:
\[\iota_i: (z_0, \dotsc, z_{i - 1}, z_{i + 1}, \dotsc, z_n) \longmapsto (z_0, \dotsc, z_{i - 1}, 1, z_{i + 1}, \dotsc, z_n)\]
座標変換 \({\varphi_i \circ \varphi_j\inv}\) を確かめる。\({i \gt j}\) とすると、この変換は次のようなものとなり、複素数では \(n\) 個の、実数では \(2n\) 個の座標成分があるとみなせる。
\[(z_0, \dotsc, z_{j - 1}, z_{j + 1}, \dotsc, z_n) \longmapsto \left(\frac{z_0}{z_i}, \dotsc, \frac{z_{i - 1}}{z_i}, \frac{z_{i + 1}}{z_i}, \dotsc, \frac{z_{j - 1}}{z_i}, \frac{1}{z_i}, \frac{z_{j + 1}}{z_i}, \dotsc, \frac{z_n}{z_i} \right).\]座標変換が \(C^\infty\) 級であり、\(\CC P^n\) はハウスドルフであるので、多様体である。