第 5 章 多様体上の関数(前編)¶
5.1 関数の台¶
- 関数の 台
多様体 \(M\) で定義された関数 \(f\) に対する次の部分集合のことを関数の台という。
\begin{align*} \supp{f} = \closure{\set{x \in M \sth f(x) \ne 0}} \end{align*}ノート上は集合の閉包を上線で表現してあるはず。補集合ではない。
ちなみに補集合については次のことが成り立つことに注意する:
\begin{align*} x \in M \setminus \supp{F} \iff \exists U \owns \quad\text{s.t.}\quad f(U) = \zeroset \end{align*}定義上、多様体という条件を位相空間にまで緩められる。
定理 5.1.1: 任意の \({x_0 \in M}\) とその任意の近傍 \({V \in M}\) に対して、次のような \(M\) を定義域とする \(C^\infty\) 級関数 \(\mu\) が存在する:
\({\mu(x) \ge 0}\)
\({\mu(x_0) \gt 0, \supp{\mu} \in V}\)
\(\supp{\mu}\) がコンパクトである。
証明方針: 問題 3.7.1 の関数 \(\rho(x)\) を再利用してなんとか関数 \(\mu(x)\) を構成する。
プロトタイプとして非負関数 \({\mu_0(\bm x) = \rho(1 - \norm{\bm x})}\) を定義する。
これは \({\norm{\bm x} \le 1 \implies \mu_0 \ge 0}\) を満たす。
プロトタイプを若干変形した非負関数 \({\displaystyle \mu1 = \mu0\left(\frac{2}{\eps}(\bm x - \varphi(x_0))\right)}\) を定義する。
まず \(x_0\) を含む座標近傍 \({(U, \varphi)}\) をとり、これを \(V\) との共通部分の座標の像 \({\varphi(U \cap V) \subset \RR^n}\) を思い浮かべるといい。点 \({\varphi(x_0)}\) について次を満たす \({\eps \gt 0}\) が何か存在する:
\[B_\eps(\varphi(x_0)) \subset \varphi(U \cap V).\]このボールのさらに半径が半分の(卵ならば黄身の部分)部分集合を座標とする \(V\) の点について、\({0 \le \mu_1 \le 1}\) が成りたつ。卵ならば白身の部分ではゼロとなる。
最後に \(\mu_1\) を定義域を全体に拡張すれば所望の関数が得られる:
\[\begin{split}\mu(x) = \begin{cases} \mu_1(\varphi(x)) & \quad \text{if } x \in U \cap V\\ 0 & \quad \text{if } x \in M \setminus (U \cap V). \end{cases}\end{split}\]
定理 5.1.2: \(M\) のコンパクト集合 \(K\) とそれを含む開集合 \(U\) があるとき、次のような \(M\) を定義域とする \(C^\infty\) 級関数 \(\nu\) が存在する:
\({\nu(x) \ge 0}\)
\({\nu|K(x) > 0}\)
\(\supp{\nu}\) が \(U\) のコンパクト集合である。
証明方針: 定理 5.1.1 の関数 \(\mu(x)\) をいくつか足して関数 \(\nu(x)\) を構成する。
前定理を再利用すると以下の条件が成り立つような各関数が存在する:
\[\forall x_0 \in K, \exists \fn{\mu_{x_0}}{M}\RR \quad \text{s.t.} \quad \forall x \in M, \mu_{x_0}(x) \le 0, \mu_{x_0}(x_0) > 0, \supp \mu_{x_0} \subset U.\]\(\set{x \in M \sth \mu_{x_0}(x) \gt 0} = \operatorname{int}(\supp \mu_{x_0})\) であることに注意。\(K\) のコンパクト性により、次が成り立つ:
\[\exists x_1, \dotsc x_k \quad \text{s.t } K \subset \bigcup_{i = 1}^k \operatorname{int}(\supp \mu_{x_i}).\]最後に和を取れば所望の関数となる: \({\displaystyle \sum_{i = 1}^k \mu_{x_i}(x).}\)
定理 5.1.3: 定理 5.1.2 と同じ仮定の下で次のような \(M\) を定義域とする \(C^\infty\) 級関数 \(\nu\) が存在する:
\({0 \le \nu(x) \le 1}\)
\({\nu|K(x) = 1}\)
\(\supp{\nu}\) が \(U\) のコンパクト集合である。
証明方針:
前定理の性質を満たす関数 \(\fn{\nu_1}{M}\RR\) をとる。
\({K = \supp \nu_1 \setminus \operatorname{int}(\supp \nu_1)}\) は開集合 \({U \setminus K}\) のコンパクト部分集合である。
繰り返し前定理を再利用し、関数 \(\fn{\nu_2}{M}\RR\) がとれる。 \({(\nu_1 + \nu_2)|\supp \nu_1 > 0}\) より次の関数を考える:
\[\begin{split}\nu(x) = \begin{cases} \displaystyle \frac{\nu_1}{\nu_1 + \nu_2} & \quad \text{if } x \in \operatorname{int}(\supp(\nu_1 + \nu_2))\\ 0 & \quad \text{if } x \in M \setminus \operatorname{int}(\supp(\nu_1 + \nu_2)). \end{cases}\end{split}\]これは所望の条件をすべて満たす。
注意 5.1.4 の \({\fn{\nu f}{M}\RR,\ \nu|K = f|K}\) の意味は、このあとの方向微分の問題で効いてくる。
ここまでの議論で、多様体上には多くの \(C^\infty\) 級関数が存在することがわかった。
補題 5.1.5: アダマールの補題
\(\RR^n\) 内の原点の開近傍で定義されている \(C^\infty\) 級関数 \(f\) に対して、次のように書けるような \(C^\infty\) 関数 \({g_k\ (k = 0, \dotsc, n)}\) が存在する:
\begin{align*} f(x_1, \dotsc, x_n) & = f(0, \dotsc, 0) + \sum_{k = i}^{n}x_i g_i(x_1, \dotsc, x_n)\\ \frac{\partial f}{\partial x_k}(0, \dotsc, 0) & = g_k(0, \dotsc, 0) \end{align*}初等的な方法で示せる。\({ \displaystyle g_k(x_1, \dotsc, x_n) = \int_0^1 \frac{\partial f}{\partial x_k} (tx_1, \dotsc, tx_n)\,\dd{t}}\)
問題 5.1.6: 方向微分
多様体 \(M\) 上で定義されている \(C^\infty\) 級関数 \(f, g\) と点 \({p \in M}\) に対して、線形な演算 \(D\) が定義できて \({D(f \cdot g)} = {Df g(p) + f(p) Dg}\) が成り立つとする(これを方向微分と呼ぶ)。
点 \({p \in M}\) における方向微分全てからなる空間 \(\mathcal{D}_p\) は実ベクトル空間である。
解答にあるように、\({D_1, D_2 \in \mathcal D_p,}\quad {a_1, a_2 \in \RR}\) に対して \({(a_1 D_1 + a_2 D_2)(fg)} = {(a_1 D_1 + a_2 D_2)f g(p) + f(p) (a_1 D_1 + a_2 D_2) g}\) を示せばよい。
多様体 \(M\) 上の曲線 \({c(t)\ (c(0) = p)}\) について \({\displaystyle D_c: f \longmapsto \diff{(f \circ c)}{t}(0)}\) は点 \(p\) における方向微分である。
これも計算だけで済む。次の二点を確認すればよい:
\[\begin{split}&&D_c(a_1 f_1 + a_2 f_2) = a_1 D_c(f_1) + a_2 D_c(f_2)\\ &&D_c(fg) = D_c(f)g(0) + D_c f(0)(g)\end{split}\]
\(\mathcal{D}_p\) の基底は \(\displaystyle \Set{ \left(\frac{\partial}{\partial x_1} \right)_p, \dotsc, \left(\frac{\partial}{\partial x_n} \right)_p}\) である。
ここで \({\displaystyle \left(\frac{\partial}{\partial x_k} \right)_p}\) とは曲線 \({\displaystyle t \longmapsto \varphi\inv(0, \dotsc, \overset{(k)}t, \dotsc, 0)}\) における方向微分とする (cf. p. 76)。
\(Df\) が点 \(p\) の近傍で定義された \(C^\infty\) 級関数に対して定義されることを示す。この際に 定理 5.1.3 の関数 \(\nu\) および 注意 5.1.4 の事実を用いる。
\({D \in \mathcal D_p}\) が上述の一次結合で表されることを示す。 \({f \in C^\infty(M)}\) に対して \({\displaystyle \left(\frac{\partial}{\partial x_i} \right)_p f} = {\frac{\partial(f \circ \varphi\inv)}{\partial x_i}(0, \dotsc, 0).}\)
\({(\nu f) \circ \varphi\inv}\) を \(\RR^n\) 上の関数とみなして、アダマールの補題を適用して次のような \({g_i}\) を定義する(これ合っているか?):
\[\begin{split}\begin{align*} &(\nu f) \circ \varphi\inv = f(p) + \sum_{i = 1}^n x_i g_i(x_1, \dotsc, x_n),\\ &g_i(0, \dotsc, 0) = \frac{\partial(f \circ \varphi\inv)}{\partial x_i}(0, \dotsc, 0). \end{align*}\end{split}\]点 \(p\) の近傍では \({\displaystyle f = f(p) + \sum_{i = 1}^n (x_i \circ \varphi\inv)(g_i \circ \varphi\inv)}\) となっている。よって次のようにすれば線形結合になっていることが示される:
\[\begin{split}\begin{align*} Df &= D(f(p)) + \sum_{i = 1}^n (D(x_i)g_i(0) + 0 \cdot D(g_i))\\ &= \sum_{i = 1}^n D(x_i)\frac{\partial(f \circ \varphi\inv)}{\partial x_i}(0, \dotsc, 0)\\ &= \sum_{i = 1}^n D(x_i) \left(\frac{\partial}{\partial x_i} \right)_p f. \end{align*}\end{split}\]
最後に各基底の一次独立性を示しておく。
\[\left(\frac{\partial}{\partial x_i} \right)_p x_j = \left(\frac{\partial x_j}{\partial x_i} \right)(0, \dotsc, 0) = \delta_{ij}.\]
ヒントをどこで利用したのかを分かりやすくしておきたい。
\({D(const) = 0.}\)
\(Df\) は関数 \(f\) の点 \(p\) の近傍の値(だけ)で決まる。
点 \(p\) の近傍で定義されている任意の関数 \(f\) に対して、 \({V \subset U}\) 上 \(f\) に一致する \(C^\infty\) 級関数がある。
5.2 コンパクト多様体のユークリッド空間への埋め込み¶
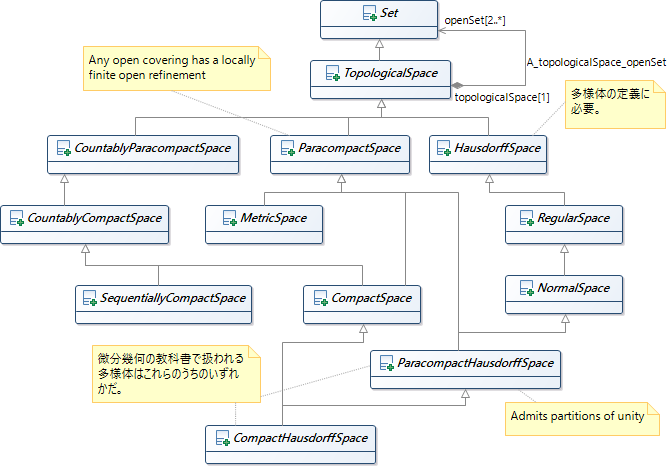
本書で扱われる位相空間各種の関係を、現時点では未登場のものも含んで、ここで図式化しておく:
例題 5.2.1: コンパクトハウスドルフ空間は 正規空間 である。
位相空間論の教科書を参照する。
まず 正則空間 であること、すなわち一点 vs 閉集合について証明する。
実はパッと読んだ時点で「?」だったが、有限開被覆 \(\set{U_{y_i}}\) の各開集合の点 \(y_i\) に対応して被覆 \({V_{y_i} \owns x_0}\) が決まるということが気付かなかっただけだった。
それから普通の閉集合 vs 閉集合について証明する。
例題 5.2.2: コンパクトハウスドルフ空間 \(X\) の開被覆 \(\set{U_i}\) に対し、次のような開被覆 \(\set{V_i}\) が存在する: \({V_i \subset \closure{V_i} \subset U_i}\)
位相空間論の教科書を参照する。証明方針は次のような感じだ:
コンパクト性により、有限開被覆 \(\set{U_1, \dotsc, U_k}\) が \(\set{U_i}\) から選べる。
帰納法の部分のメモ
\(V_1, \dotsc, V_{j - 1}\) が \({\closure{V_p} \subset U_p\ (p = 1, \dotsc, j - 1)}\), \({\displaystyle X = \bigcup_{i = 1}^{j - 1}V_i \cup \bigcup_{i = j}^k U_i}\) が成り立っていると仮定する。
閉集合 \({ \displaystyle K_j = X \setminus \left(\bigcup_{i = 1}^{j - 1} V_i \cup \bigcup_{i = j + 1}^k U_i\right) \subset U_j}\) を考える(部分となることは式を展開すると納得できる)。
\({K_j \cap (X \setminus U_j) = \varnothing}\) だから(集合の部分からその集合を差し引くのだから)、例題 5.2.1 で見た正規空間の性質によって次のような開集合 \(V_j, W_j\) が(帰納法により)存在する: \({K_j \subset V_j, X \setminus U_j \subset W_j, V_j \cap W_j = \varnothing.}\)
このとき \({\closure{V_i} \subset U_i}\) かつ \({\displaystyle X = \bigcup_{i = 1}^j V_i \cup \bigcup_{i = j + 1}^k U_i}\) となっている。
定理 5.2.3: コンパクト多様体はユークリッド空間に埋め込める。
ポイント: 例題 5.2.2 の開被覆の構成手順を二重に行う。つまり \({\closure{V_i} \subset U_i,\ \closure{W_i} \subset V_i}\) のようなものを取る。これらの有限開被覆の個数を \(k\) としておく。
閉集合 \(\closure{V_i}\) に関して 定理 5.1.3 の条件を満たす \(C^\infty\) 級関数 \(\nu_i\) を取る。
閉集合 \(\closure{W_i}\) に関して 定理 5.1.2 の条件を満たす \(C^\infty\) 級関数 \(\mu_i\) を取る。
座標近傍 \({(U_i, \varphi_i)}\) の局所座標 \({\varphi_i = (x_1^{(i)}, \dotsc, x_n^{(i)})}\) に対して関数 \({\nu_i \varphi_i \coloneqq (\nu_i x_1^{(i)}, \dotsc, \nu_i x_n^{(i)})}\) を取ると、これは \(C^\infty\) 級となる。
ここで \({\varPhi = (\mu_1, \nu_1 \varphi_1, \dotsc, \mu_k, \nu_k \varphi_k)}\) とおくと、これが多様体から \(\RR^{k(n + 1)}\) への埋め込みとなる:
定理 4.4.2 の上にある説明により \(\fn{\varPhi_*}{T_xM}\RR^{k(n + 1)}\) のランクが \(n\) で \(\varPhi\) が単射であるから。
ランクが \(n\) であることは \({(\nu_i \varphi_i | V_i) \circ \varphi_i\inv} = {\id_{\varphi_i(V_i)}}\) から示せる。
単射であることは \({\varPhi(x) = \varPhi(y) \implies x = y}\) を示すのに \(\mu_i\) の成分と \(\nu_i\) の成分の単射性を別々に示す。関数の非ゼロ性と局所座標の同相性が使えるので容易に示せる。
ユークリッド空間が利用できるようになったので、内積の話題が出て来るようになる。
- 法束
\({\nu M = \set{(x, v) \in \RR^N \times \RR^N \sth v \perp T_xM}}\)
これはユークリッド空間内の \(N\) 次元多様体になっている。
- 法空間
\({\nu_x M = \set{v \in \RR^N \sth v \perp T_xM }}\)
TODO: (pp. 96-97) の可換図式を何とかここに描きたい。
接束 \(TM\) が \({(V_i \times \RR^n, \gamma_{ij} \times D\gamma_{ij})}\) から構成されたのと似て、法束 \(\nu M\) は \({(V_i \times \RR^{N - n}, \gamma_{ij} \times A_{ij})}\) から構成される。ここで \({A_{ij_{(x_j)}} \in GL_{N - n}(\RR)}\) である。
注意 5.2.4
ユークリッド空間 \(\RR^{n + 1}\) 内の \(n\) 次元コンパクト多様体の法束は一次元ベクトル空間をファイバーとするベクトル束である。
ユークリッド空間 \({\RR^{n + 1} \quad(n \le 2)}\) 内の \(n\) 次元コンパクト多様体は向き付け可能とある。理屈が飲み込めない。
問題 5.2.5: ユークリッド空間 \(\RR^N\) に埋め込まれる \(p\) 次元コンパクト多様体 \(M\) の性質
法束は \(N\) 次元多様体になっている。
\({X = \nu M = \set{(\bm x, \bm y) \in \RR^{2N} \sth \bm x \in M, \bm y \perp T_{\bm x}M}.}\)
問題 4.5.3 でやったように \(M\) のグラフ表示を考えることから始める。同じような記号を使う。
\({(\bm x, \bm y) \in X \iff \bm y = (\bm y_1, \bm y_2)}\) とは、次が成り立つことと同値である:
\[\begin{split}\begin{align*} &\bm x_2 = g(\bm x_1),\\ &\begin{pmatrix}\bm y_1 & \bm y_2\end{pmatrix} \begin{pmatrix}I_p \\ Dg\end{pmatrix} = \bm 0. \end{align*}\end{split}\]\(X\) は \({(\bm x_1, \bm x_2) \longmapsto (g(\bm x_1), -\bm y_2 Dg_{(\bm x_1)})}\) のグラフとして表されている。よってこの空間は多様体である。
写像 \({e: (\bm x, \bm y) \longmapsto \bm x + \bm y}\) は \({X \cap (\RR^N \times \zeroset)}\) 近傍で微分同相である。
先ほどのグラフの写像を \(F\) とすると \({(e \circ F)(\bm x_1, \bm y_2) = (\bm x_1 - \bm y_2 Dg_{\bm x_1}, g(\bm x_1) + \bm y_2).}\)
\({\bm y_2 = 0}\) すなわち \({(\bm x_1^0, \bm 0)}\) における微分は次のようになる:
\[\begin{split}\begin{pmatrix} I_p & -{}^t\!Dg_{(\bm x_0^1)}\\ Dg_{(\bm x_0^0)} & I_{N - p} \end{pmatrix}.\end{split}\]この行列の右上のブロックと左下のブロック(第 \(i\) 列と第 \({p + j}\) 列)が直交するので、これはランクが \(N\) である。
写像 \(e\) を \({\bm y_2 = \bm 0}\) に制限した写像は 例題 4.3.1 の仮定をみたすので、主張の近傍で微分同相となる。
5.3 \(C^\infty\) 級写像と多様体の埋め込み、はめ込み¶
<どのような次元のユークリッド空間に埋め込まれるかというのは多様体の複雑さをはかる量になる> (p. 98)
例 5.3.1: 色々なコンパクト多様体
円周、球面は当然ユークリッド空間 \(\RR^2\) と \(\RR^3\) にそれぞれ埋め込まれる。
\(\RR P^2\) は \(\RR^3\) に埋め込めない。メビウス帯を部分空間として含むことによる。
<埋め込みやはめ込みの空間は、数学的に非常に興味深い> (p. 99)
例 5.3.2: 円周 \(S^1\) の埋め込み
円周の \(\RR^2\) への埋め込みは円板 \(D^2\) を囲む。\(D^2\) の \(\RR^2\) への埋め込みの境界への制限(ジョルダンの閉曲線定理)。
円周の \(\RR^3\) への埋め込みは制限とはならない。分類=結び目理論。
円周の \(\RR^n\ (n \le 4)\) への埋め込みは円板 \(D^2\) の \(\RR^n\) への埋め込みの境界への制限。
多様体の形を理解するには、超球面 \(S^n\) などのよくわかる多様体から構成的に理解するのがよい。
コンパクト連結一次元多様体は \(S^1\) と微分同相。
コンパクトではない可分な連結一次元多様体は \(\RR\) と微分同相。
コンパクト連結二次元多様体
向き付け可能: \(S^2, T^2, \Sigma_2, \Sigma_3, \Sigma_4, \dots\); 有向閉曲面は可算個。
有向閉曲面 \({\Sigma_k \subset \RR^3}\) の定義は p. 100 を参照。
向き付け不可能: \(\RR P^2, K, N_3, N_4, \dots\); 非有向閉曲面は可算個。
\({\forall x \in \Sigma_k, -x \in \Sigma_k}\) なので同値関係を定義して \({\Sigma_k/\sim}\) を定義できる。このとき、これは多様体となり非有向閉曲面 \(N_{k + 1}\) となる。
<写像 \(\fn{F}{M}N\) が与えられ、\(N\) の形と \({F\inv(y)\ (y \in N)}\) の形が理解できれば、\(M\) の形がわかることが期待できる> (p. 101)
写像 \(F\) については \(\fn{F_*}{T_xM}T_{F(x)}N\) のランクが \({\dim N}\) であるようなものがよいと思われる。こういう \(x\) とそれに対応する \(y\) はそれぞれ正則点、正則値であるという。
言葉に引っ張られないように。正則「値」と言っても多様体上の点を指している。
正則値の逆像 \({F\inv(y)}\) は \({\dim M - \dim N}\) 次元部分多様体である。
臨界点とは、正則点でない点である。
臨界値とは、臨界点全ての集合の像である。
\({\dim M \lt \dim N}\) のときは、\({F(M),\ N \setminus F(M)}\) がそれぞれ臨界値、正則値である。正則値の逆像は空集合になる。
例 5.3.4: 例題 2.4.1 の関数の検討
例 5.3.5
例題 5.3.6: 1 の分割
\(M, \set{(U_i, \varphi_i)}\) をそれぞれコンパクト多様体とその座標近傍系とする。
\(\exists \fn{\lambda_i}{M}\RR\quad\text{s.t.}\quad\lambda_i \in C^\infty(M),\ 0 \le \lambda_i(x) \le 1,\ \supp{\lambda_i} \subset U_i.\) 有限個の添字を除いて \({\lambda_i = 0,\ \sum \lambda_i = 1.}\)
証明では 例題 5.2.2 およびその元となる各種命題を利用している。\(U_i\) 上にある性質の関数 \(\mu_{i_j}\) を構成して、次のような開被覆および関数を構成する:
\begin{gather*} \lambda_{i_{i_j}} = \frac{\mu_{i_j}}{\displaystyle \sum_{l = 1}^k \mu_{i_l}},\ \set{U_{i_j}},\ \closure{V_{i_j}} \subset U_{i_j},\ \mu_{i_j}|\closure{V_{i_j}} > 0,\ \supp \mu_{i_j} \subset U_{i_j}. \end{gather*}