第 6 章 多様体上のフロー(前編)¶
値が十分近い二つの正則値同士の逆像もまた十分近い形をしているだろうか。
6.1 多様体の部分集合の比較、アイソトピー¶
微分同相写像で互いに写り合う多様体同士を同じものと考える (p. 123)。
- アイソトピー
\({t \in [0, 1]}\) に対して連続的に変化する微分同相写像 \(\fn{F_t}{M}M\) で、\({F_0 = \id_M}\) を満たすものをアイソトピーという。
\({\RR \times M}\) の \({[0, 1] \times M}\) への制限。
\(A_0, A_1 \subset M\) は多様体の部分集合であるとすると、 \({F_0(A_0) = A_0,\ F_1(A_0) = A_1.}\)
制限なしの \(F\) について
\({(t_0, x_0)}\) を固定すると \({T_{F_{t_0}(x_0)}M}\) の接ベクトルが定まる。なぜなら \({F_t(x_0)}\) が \({F_{t_0}(x_0)}\) を通過するから。
\({\forall y_0 \in M, x_0 = F_{t_0}\inv(y_0)}\) とすると \({T_{y_0}M}\) の接ベクトルが定まる。なぜなら \(F_{t_0}\) が微分同相だから。
\({X_t \coloneqq \fn{\dfrac{\partial F_t}{\partial t} \circ F_t\inv}{M}T_{y_0}M}\) なる量を考える。
\({y_0 \in M}\) 周りの座標近傍を \({(U, \varphi)}\) とし、
\({\varphi \circ (F_t \circ F_{t_0}\inv)\circ\varphi\inv(x_1, \dotsc, x_n)}\) を \({(f_1(t, t_0, x_1, \dotsc, x_n), \dotsc, f_n(t, t_0, x_1, \dotsc, x_n))}\) と書く。
\({\displaystyle X_i = \sum_{i = 1}^n \diff{f_i}{t}(t, t_0, x_1, \dotsc, x_n) \frac{\partial}{\partial x_i}.}\)
\({(t_0, \varphi(y_0))}\) の近傍で定義されている \(\RR^n\) に値を持つ \(C^\infty\) 級写像である。
\({(t_0, \varphi(y_0))}\) の近傍において \({X(t, y) = X_t(y)}\) による写像 \(\fn{X}{\RR \times M}TM\) は \(C^\infty\) 級写像である。
- ベクトル場
各 \(t\) について \(\fn{X_t}{M}TM\) は \({p \circ X_t = \id_M}\) となる \(C^\infty\) 級写像である。
そこで、こういう性質を持つ \(C^\infty\) 級写像 \(\fn{X}{M}TM\) を \(M\) 上の \(C^\infty\) 級ベクトル場と言う。
\({\displaystyle \diff{F_t}{t} = X_t \circ F_t,\ F_{t_0} = \id_M}\)
\({F_{t_0} = \id_M}\) となる \(F_t\) により \({F_{t_1}(A_0) = A_1}\) となることは、ベクトル場の定める常微分方程式の解により \(A_0\) を \(A_1\) に写すことと同じである。
\({t = t_0}\) のとき \({F_t \circ F_{t_0}\inv}\) を局所座標表示するとわかる。
例 6.1.1: 線形常微分方程式を \(\RR^n\) 上の接ベクトルとして書く。
以下 \({A(t) \in M_n(\RR)}\) を \(t\) について連続な行列、成分を \({A(t) = (a_{ij}(t))}\) と表し、ベクトル \({\bm{x} = (x_j)}\) と表す。
\({\displaystyle \diff{}{t}\bm{x} = A(t)\bm{x}}\) について、これは接ベクトル場 \({\displaystyle \sum_{i = 1}^n\left(\sum_{j = 1}^n a_{ij}(t)x_j\right)\frac{\partial}{\partial x_i}}\) である。
\(A(t)\) が \(t\) に非依存ならば \({F_t \circ F_{t_0}\inv(\bm{x}) = e^{(t - t_0)A}\bm{x}}\) である。
例題 6.1.2: 微分同相からアイソトピーを構成する?
仮定
\(\fn{F}{\RR^n}\RR^n\) は微分同相であり、
\({DF_{(\bm{x})} - I_n}\) の成分の絶対値が \({\displaystyle \eps\quad (\lt \frac{1}{2n})}\) より小さいとする。
結論(ただし本書の関数定義には誤植があると思われるので勝手に修正する)
\({F_t(\bm{x}) = (1 - t) \bm{x} + t F(\bm{x})}\) は微分同相であり、
\({F_0 = \id_{\RR^n},\ F_1 = F}\) である。
証明
\(DF_{(\bm{x})}\) は正則である。
単純計算により \({DF_{(\bm x)} = (I_n + t(DF_{(\bm{x})} - I_n)).}\)
高校数学の \({\displaystyle \frac{1}{1 + x}}\) の級数展開を参考に次の式が浮かぶ:
\begin{gather*} (I_n + t(DF_{(\bm{x})} - I_n))\sum_{k = 0}^\infty (-t)^k (DF_{(\bm{x})} - I_n)^k = I_n \end{gather*}問題は級数の収束性だが(行列式の評価には注意したい)、これは仮定の評価から絶対収束であることがわかる:
\begin{split} \abs{(-t)^k (DF_{(\bm{x})} - I_n)^k} &<& \abs{t^k n^{k - 1} \eps^k}\\ &<& n^{k - 1} \eps^k\\ &<& \frac{1}{2^{k - 1}}\eps. \end{split}以上で \(DF_{(\bm x)}\) の逆行列が存在して、それが上記の級数で与えられることがわかった。
\(F_t\) は単射である。
\({H_t(\bm{x}) = \bm{x} - F_t(\bm{x})}\), \({\bm{y} \in \RR^n}\) とおくと次のように評価できる:
\begin{split} \norm{H_t(\bm{x}) - H_t(\bm{y})} & \le nt\eps \norm{\bm{x} - \bm{y}}\\ & \le \frac{1}{2}\norm{\bm{x} - \bm{y}}\\ \therefore \norm{F_t(\bm{x}) - F_t(\bm{y})} & \ge \frac{1}{2}\norm{\bm{x} - \bm{y}} \end{split}\(F_t\) は全射である。
\({\bm{x_1} = \bm{y},}\ {\bm{x}_{k + 1}} = {\bm{x}_k - (F_t(\bm{x}_k) - \bm{y})} = {\bm{y} + H_t(\bm{x}_k)}\) とおく。次のように評価できる:
\begin{split} \norm{\bm{x}_{k+1} - \bm{x}} & \le& \frac{1}{2^{k-1}}\norm{\bm{x}_2 - \bm{x}_1}\\ & =& \frac{1}{2^{k-1}}\norm{\bm{y} - F_t(\bm{y})}\\ &\therefore& \bm{x}_k \to \bm{y}\ \text{s.t. } \bm{y} = F_t(\bm{y}). \end{split}
6.2 フロー¶
序盤から難しい。ベクトル場とフローの関係を図に示してみる。ベクトル場は接束の切断であると理解できる。
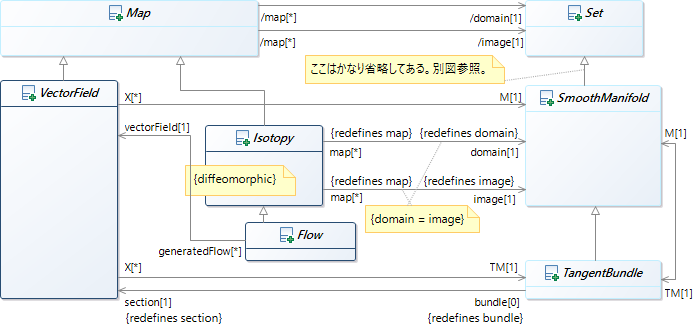
- フロー
フローとは次の性質を満たすアイソトピーである: \({F_s \circ F_t = F_{s + t}.}\)
フローは加法群 \(\RR\) の多様体への群作用である。
ベクトル場 \(X_t\) は、あるいは局所座標系で書かれた常微分方程式は \(t\) に依存しない。
\(F_t\) がフローの場合は \({\displaystyle X_{t_0}(y_0) = \frac{\partial F}{\partial t}(t_0, F_{t_0}\inv(y_0)) = \frac{\partial F}{\partial t}(0, y_0) = X_0(y_0)}\) とあるが、二番目の等号が成立する根拠がわからない。\({F_t = F_{t - t_0} \circ F_{t_0}}\) であることがどう関わっているのか。
ベクトル場 \({X = X_t}\) はフローを \(F_t\) を生成するベクトル場であるという。生成の主従を逆に見ることもある。
例 6.2.1: 軌道
\(\RR^n\) のベクトル \({\bm x = (x_i)}\) と行列 \({A = (a_{ij})}\) を考える。
\({F_t(\bm x) = \mathrm{e}^{tA} \bm x}\) は \(\RR^n\) 上のベクトル場 \({\displaystyle \sum_{i = 1}^n \left( \sum_{j = 1}^n a_{ij} x_j \right)\frac{\partial}{\partial x_j}}\) が生成するフローである。
\({\displaystyle \diff{F_t}{t}\circ F_{-t} = A \mathrm e^{At\bm x} \mathrm e^{-At\bm x} = A\bm x = \sum\sum a_{ij}x_j.}\)
フロー \(\set{ F_t(\bm x) \sth t \in \RR}\) を \(\bm x\) を通る軌道という。この軌道は \(M\) 上の同値関係を定義する。
軌道は一点、円周、実数全体のいずれかでパラメーター付けられる。
円周ならば一次元部分多様体である。
例 6.2.2: 平面上の線形ベクトル場の生成するフローの軌道カタログ
式にすれば \({\displaystyle \sum_{i, j = 1}^2 a_{ij} x_j \frac{\partial}{\partial x_j}}\) だが、本書の図によると三種類に分類できるようだ。
問題 6.2.3: コンパクト多様体上のフローについて
\({\varphi_{t_1}(x_0) = \varphi_{t_2}(x_0)}\) ならば \({\exists T \le 0,\ \exists n \in \ZZ \ \text{s.t. } t_2 - t_1 = nT.}\)
まとめて考えるために \({A = \set{t \in \RR \sth \varphi_t(x_0) (= \varphi_0(x_0)) = x_0} \subset \RR}\) とおく。\(A\) が群であることと、閉集合であることを示す:
\({0 \in A}\)
\({a_1, a_2 \in A}\) について \({\varphi_{a_1 + a_2}(x_0) = \varphi_{a_1} \circ \varphi_{a_2}(x_0) = \varphi_{a_1}(x_0) = x_0}\) だから \({a_1 + a_2 \in A.}\)
よって \(A\) は \(\RR\) の部分群となっている。
閉集合であることを示すために \(A\) の収束点列の極限が \(A\) にあることを示す。
\(\varphi_t(x_0)\) は \(t\) について連続であるので、点列 \(\set{a_i}\) が \({\displaystyle \lim_{i \to \infty} a_i = a}\) とおくと、次のようになる:
\[\varphi_a(x_0) = \lim_{i \to \infty}\varphi_{a_i}(x_0) = \lim_{i \to \infty}x_0 = x_0.\]
したがって \(A\) は \(\RR\) の閉集合となっている。
\({A = \zeroset}\) と仮定すると \({T = 0}\) が求める値となる。
\({A \ne \zeroset}\) と仮定すると \({T = \inf\set{a \in A \sth a \gt 0}}\) が求める値である。要するに \(A\) の中でゼロの次に小さい値である。
\({T > 0}\) のときは \({A = \ZZ T}\)
\({A \in \ZZ T, \exists n\ \text{s.t. } \abs{a - nT} < T}\) しかし \({a - nT \in A \implies a = nT.}\)
\({T = 0}\) のときは \({A = \RR}\)
さっきと同じように \({\set{a_i} \in A, a_i > 0, \lim a_i = 0 \implies \bigcup\set{n a_i \sth n \in \ZZ} \subset \RR}\) は稠密であるが、\(A\) が閉集合であるために \({A = \RR.}\) \({\therefore t \in \RR,\ \varphi_t(x_0) = x_0.}\) これは仮定の「定数関数ではない」に反する。
となる。
\({\exists y \in M,\ \text{s.t. } \forall U_y \owns y, \sup\set{t \in \RR \sth \varphi_t(x_0) \in U_y} = \infty.}\)
\({\varphi_t(x_0) = x_0, t \ne 0}\) ならば \({y = x_0}\) である。
そうでなければ \(\set{\varphi_t(x_0) \sth t \in \NN}\) の集積点を \(y\) とする。
この問題が言いたいことは図を描いて理解するのがいい?