基本テク

本稿では Matplotlib インストール直後にでも実現可能な基本的な操作について記す。基本の手順は、NumPy/SciPy の機能でデータを生成し、その 2D プロットを Matplotlib を用いて描画することだ。

Note

特に断らない限り、以降のテキストおよびコード片においては、各種 import を次のようにしたものと仮定している。

import numpy as np
import scipy as sp
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib import pylab, mlab

基本的な関数・メソッドを押さえる

下の表を見てからヘルプを当たる。

後で見るように、モジュール matplotlib.pyplot の関数の機能は、ある種の「アクティブな」オブジェクトのメソッド呼び出しをするだけに過ぎない。

関数

機能

plt.plot(...)

グラフを描く

plt.hist(...)

ヒストグラムを描く

plt.show(...)

イメージを一気に表示

plt.savefig(...)

イメージをファイルに保存

plt.setp(...)

プロット線の属性等、描画パラメーターの取得・指定

plt.axis(...)

ビューポート範囲指定

plt.grid(...)

グリッド描画をするかしないか指定

IPython を利用している場合はおもむろに plt? とタイプするのもお勧めだ。 Matplotlib の概要がサインカーブのプロットを表示する簡素な例とともにコンソールに出力する。

Figure と Axes の概念を理解する

Matplotlib には current figure と current axes という概念がある。これを利用して、複数個のグラフをワンシーンに定義できるようだ。

関数

機能

plt.figure(...)

指定の figure をカレントにする

plt.subplot(...)

指定の axes をカレントにする
Figure

大抵の本にはいくつかの図がしばしばキャプション付きで載っている。Figure という語は、それに対応するクラスだと解釈したい。図の一つ一つが Figure のオブジェクトになると思えば、個人的にはコードが理解できる。

Axes

普通は一つの図にグラフ一つを載せるわけだが、同じようなグラフを並べたものを一つの図としたい場合もある。 Axes という語が意味するのが、そのグラフだと解釈すればよいか。

余談だが MS Word のグラフ API にも Axes というコンセプトがあったと記憶している。

次の図にふたつの Axes を持たせたひとつの Figure を示す。

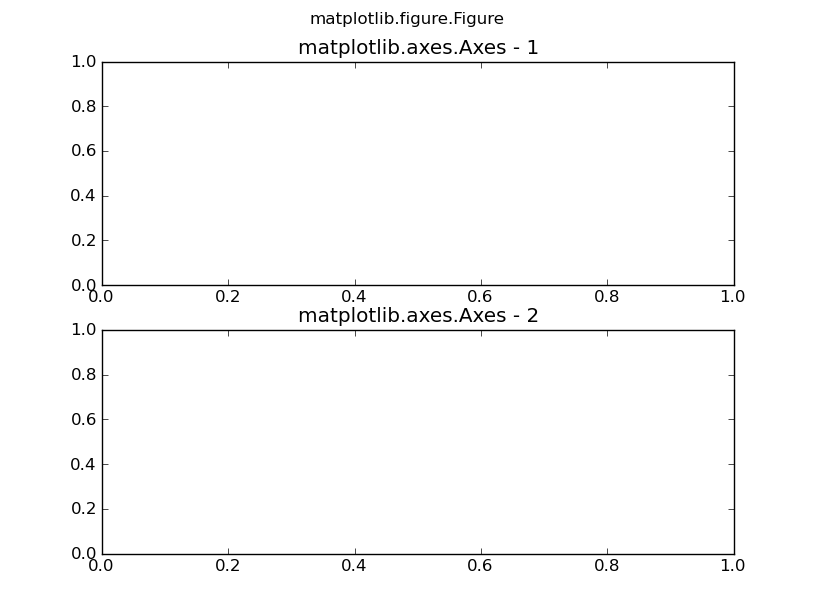
Axes デモ

  • plt.figure(n) で current figure を指定する。

  • plt.subplot(n0n1n2) で current axes を指定する。n0, n1, n2 がそれぞれ縦方向の区画数、横方向の区画数、「どの区画か」を意味する。

    n2 は 1 以上 n1 * n2 以下の値でなければならない。

  • plt のプロットコマンドはすべて current axes に作用する。

    import matplotlib as mpl
import matplotlib.pyplot as plt

# Make figure-1 active and get it.
fig = plt.figure(1)

# Split the active figure into 2x1 (2 rows and 1 column)
# and make axes-1 active.
plt.subplot(211)

# ...
# All plotting commands here are applied to axes-1.

# Split the active figure into 2x1
# and make axes-2 active.
plt.subplot(212)

# ...
# All plotting commands here are applied to axes-2.

  • Matplotlib は figure/axes を扱うスタイルを二つ提供している。

    • 古典的なステートマシン様式

      ユーザーコードがカレントな figure/axes が何であるかを常に意識して、プロットコマンドを呼び出す。コマンドはカレントな figure/axes に対して適用されることになる。

    • 状態とオブジェクトとを関連付けて取り扱うオブジェクト指向プログラミング様式

      figure/axes がオブジェクトになっていて、メソッドでプロットコマンドを呼び出す。コマンドは対象となるオブジェクトの管理する figure/axes に対して適用されることになる。

テキストを使う

当ノートの目的のひとつに、「数式を含むテキストを表示する」ことがある。そのためには、事前に単純ななテキスト描画の方法を学習する必要があるだろう。モジュール plt からテキストに強く関連していそうな機能を表にしてみよう。

関数

機能

plt.text(...)

ビューポート内にテキストを描く

plt.xlabel(...)

X 軸用キャプション

plt.ylabel(...)

Y 軸用キャプション

plt.title(...)

グラフ全体のキャプション

  • plt.text() は指定位置にテキストを描画するコマンドと考える。

テキストプロパティ

個人的によく使うテキストプロパティを表にまとめておく。各種テキストコマンド関数・メソッドのキーワード引数として指定するのが一つのやり方。

キーワード

意味

color

テキストの色。

family

テキストのフォント名。フォント名を直接指定するか "sans-serif" 等の予約名を指定する。

rotation

テキストの流し込む角度。度単位で直接指定する。

size

フォントサイズをポイントで指定するか "x-large" 等の予約名を指定する。

stretch

0 から 1000 までの値を指定するか "condensed" 等の予約名を指定する。

style

"normal", "italic", "oblique" から選択。

weight

0 から 1000 までの値を指定するか "bold" 等の予約名を指定する。

  • テキストの基準位置は horizontalalignment, verticalalignment キーワード引数で指示できる。例えば x, y 引数をテキストの右下位置としたい場合には次のようにする：

    plt.text(x, y, 'aaaa', verticalalignment='bottom', horizontalalignment='right')

  • 複数行テキストの左揃え・中央揃え・右寄せを指定する場合は multialignment キーワードを使用する。

日本語のテキストを描画する

matplotlib.font_manager.FontProperties を明示的に利用する手段を見つけた。

#!/usr/bin/env python
"""japanese_text.py: Demonstrate how to draw Japanese text.
"""
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties

FONT_PROP = FontProperties(fname=r'C:\WINDOWS\Fonts\HGRME.TTC')

plt.text(0, 0, '御無礼\n一発です',
         fontproperties=FONT_PROP, fontsize=60)
plt.show()

結果のスクリーンショットは次のようなものだ。

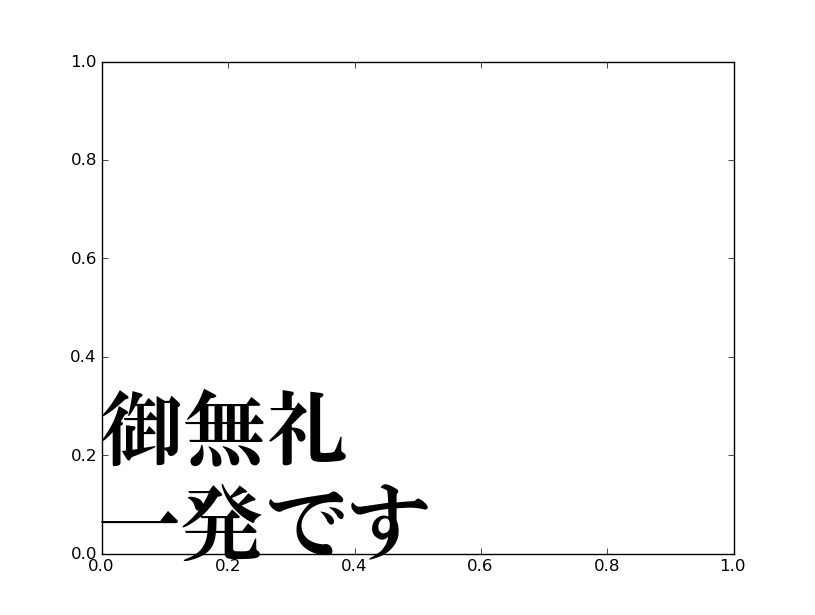
御無礼一発です

ただしフォントパスをハードコードするような手法は可搬性がない。上記の技法を本番で用いぬことだ。日本語の文字を恒常的に描画させるには、ユーザー設定ファイルでフォントを指定するのが自然だ。

  • Cygwin ならファイル $HOME/.matplotlib/matplotlib を、

  • Linux ならファイル $HOME/.cache/matplotlib/matplotlib

を開いて次の項目に日本語に対応したフォントを指定することだ：

  • font.family

  • font.sans-serif: 先頭に加える。

なお、設定ファイルのパスは環境設定のノートで述べるような仕組みで決定されるものだ。それは関数 mpl.matplotlib_fname に対する help で確認できる。

Artists 関連

  • primitives: Line2D, Rectangle, Text, AxesImage, etc.

  • containers: Axis, Axes, Figure, etc.

コンテナーを攻略していく。

  • Axes はプロッティングエリア。

  • Subplot は Axes の特別なもの。コード的にもサブクラスで表現されている。

  • Patch というクラス名は MATLAB から受け継いだ。

  • プロパティー一覧は matplotlib.artist.getp 関数で確認できる。

Figure (matplotlib.figure.Figure)

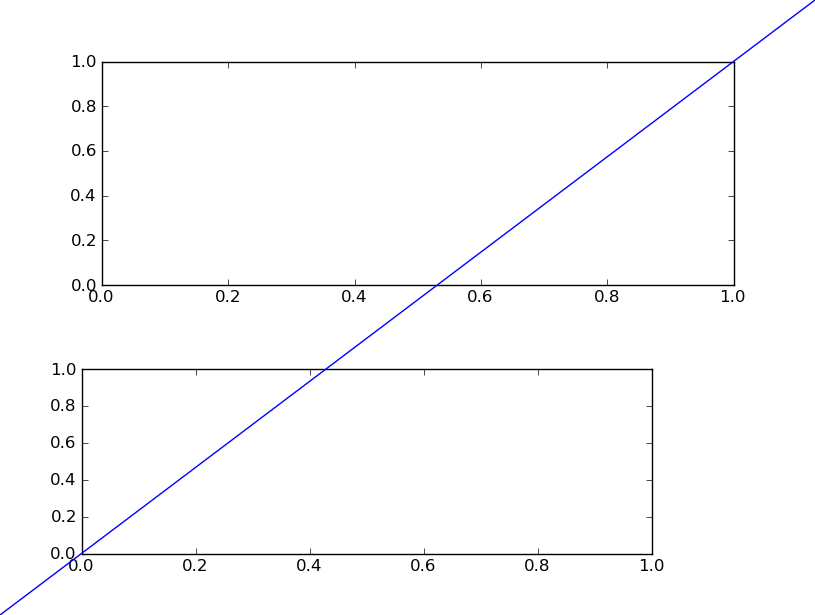
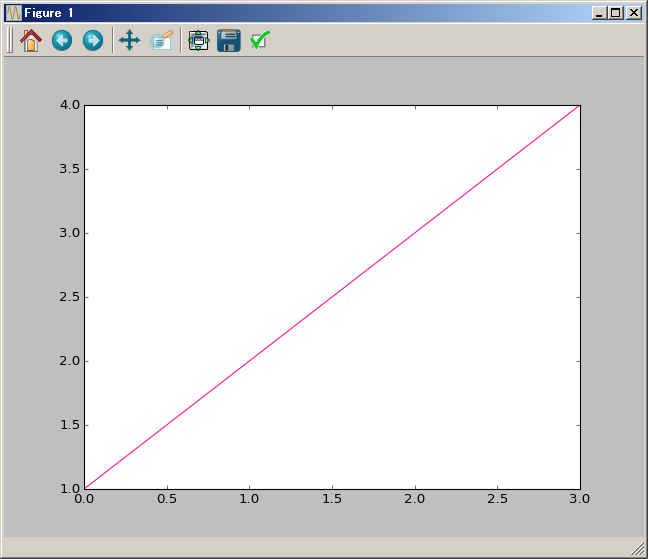
  • Figure オブジェクトが “current axes” を管理している。

  • Figure は（グラフのものではない）自身の座標系を持っていて、矩形の左下と右上がそれぞれ (0, 0), (1, 1) となっている。

    変な例だが、画像全体に対角線を一本引くにはこうする。キーワード引数 transform の値がいかにもな感じがするだろう。

    #!/usr/bin/env python
"""diagonal.py: Demonstrate how to draw a diagonal line which joins
two opposite corners of the figure.
"""
import matplotlib as mpl
import matplotlib.pyplot as plt

fig = plt.figure()

ax1 = fig.add_subplot(211)
ax2 = fig.add_axes([0.1, 0.1, 0.7, 0.3])

line = mpl.lines.Line2D([0, 1], [0, 1],
                        transform=fig.transFigure, figure=fig)
fig.lines.extend([line])
fig.canvas.draw()
plt.show()

    結果は次のスクリーンショットのようなものとなる：

    対角線

Axes (matplotlib.axes.Axes)

Axes オブジェクトが図形・テキスト・目盛・グリッド・ラベル各オブジェクトを管理する。まずコンテナーメンバーのうち、馴染みのあるものだけ表にまとめておく。

メンバー名

内容物

lines

plot 等で作成した Line2D オブジェクト。

patches

各種 Patch オブジェクト。Ellipse, Polygon, etc.

texts

text や annotate で作成した各種テキスト。

非コンテナーメンバーも少しだけ押さえておく。

メンバー名

オブジェクト

patch

Axes の背景用 Rectangle オブジェクト。

xaxis

XAxis オブジェクト。

yaxis

YAxis オブジェクト。

Axis (matplotlib.axis.Axis)

グラフの目盛、グリッド、目盛に付けるラベル等を管理する。Axes オブジェクトの xaxis および yaxis メンバーでアクセスできる。

使用頻度の高いものだけ表にしておく。

メソッド

機能

get_major_ticks

目盛 (matplotlib.ticker.Ticker) オブジェクトを返す。

grid

グリッド線を描画するしないを指示。

 
import matplotlib.pyplot as plt
ax = plt.gca()

# Modify the tickers for Y axis.
for tick in ax.yaxis.get_major_ticks():
    tick.tick1On = False   # Hide tickers on left side.
    tick.tick2On = True    # Show tickers on right side.
    tick.label1On = False  # Hide labels on left side.
    tick.label2On = True   # Show labels on right side.

バックエンド

バックエンドとは、グラフを何が何へ出力するのかを指す概念であると思う。これは公式のドキュメントの記述が完璧なので、何か気になることができたら、素直にそちらを当たるのがよい。

ユーザーインターフェイスバックエンドとハードコピーバックエンドの二種類があり、前者はウィンドウ、後者はファイル形式とおおまかに考えられる。それぞれ plt.show() と plt.savefig() の振る舞いに影響する。

ここではコードでのバックエンド設定方法を述べる。設定ファイルによる設定方法は 環境設定 を参照。

ユーザーインターフェイスバックエンド

例えば PyQt5 の UI でグラフをウィンドウに表示する場合、次のようにするとそうなる。

import matplotlib as mpl
mpl.use('Qt5Agg')

なお mpl.use 関数を呼び出すタイミングは、最初の import matplotlib の直後がベストのようだ。IPython のセッションであらかじめ matplotlib.plt 等がインポートされていて、同関数が呼び出せない状況に陥っているというのがありがちだ。

上記のコードが機能するには、環境に PyQt5 がインストール済みである必要がある。 PyQt5 利用ノート 参照。

Qt5Agg

ハードコピーバックエンド

ハードコピーバックエンドのカスタマイズはこのノートの目的の一つ。backend の値を PS, PDF, PNG, SVG のどれかにしておくと、その名前の形式のファイルを作成することができる。コードで実現するには、次のような手順にしておけばよい。

import matplotlib as mpl
mpl.use('PDF')  # We want the image as PDF file.

# ... Here come plotting commands.

plt.savefig('output')  # File output.pdf will be saved.

ヒストグラムを描く

ノートを整理していたら未使用のスクリプトを発見したので、説明なしにここにコードを記す。

#!/usr/bin/env python
"""histogram.py: Demonstrate how to show a histogram.
"""

import matplotlib.pyplot as plt
from numpy.random import randn

cur_axes = plt.gca()
_, bins, rects = cur_axes.hist(randn(1000), 50, facecolor='yellow')

for tick in cur_axes.xaxis.get_minor_ticks():
    tick.tick1On = True

for tick in cur_axes.yaxis.get_major_ticks():
    tick.gridOn = True
    tick.tick1On = False
    tick.tick2On = True
    tick.label1On = False
    tick.label2On = True

plt.show()

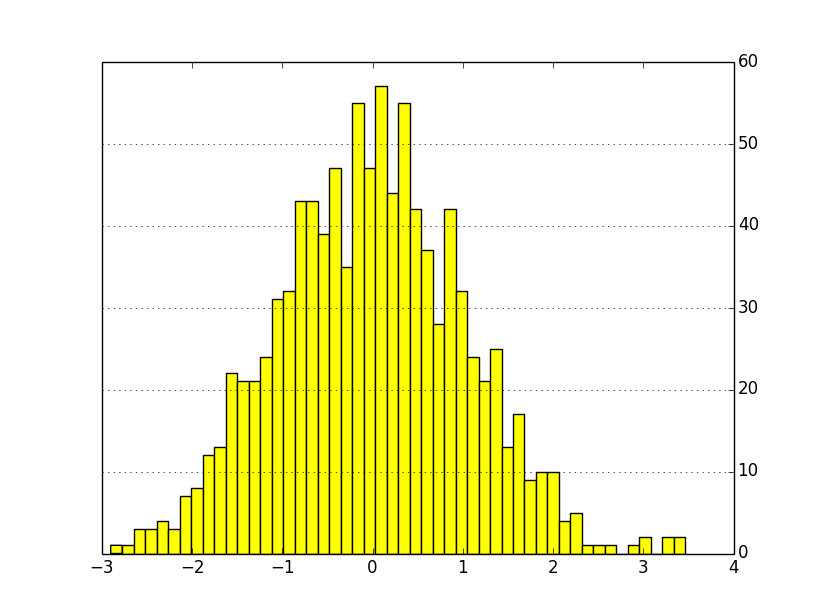
最終的な描画結果は次のようなものとなる。乱数次第で分布が変化するので注意。

ヒストグラム

曲線を描く

曲線とは言っても実際は折れ線だ。

多項式

実数 \(x\) の多項式 \(f(x)\) について \(y = f(x)\) のグラフを描きたい。次の容量で曲線を定義する。

  1. プロットする \(x\) のサンプル点を関数 numpy.arange で適宜準備する。やり方を忘れていたら NumPy 利用ノート を参照。

  2. 多項式 \(f\) を関数 numpy.poly1d の戻り値で表現する。

  3. 評価する変数を関数 np.linspace で用意する。

  4. プロットする値を np.array オブジェクトに対する broadcasting を利用して一気に得る。

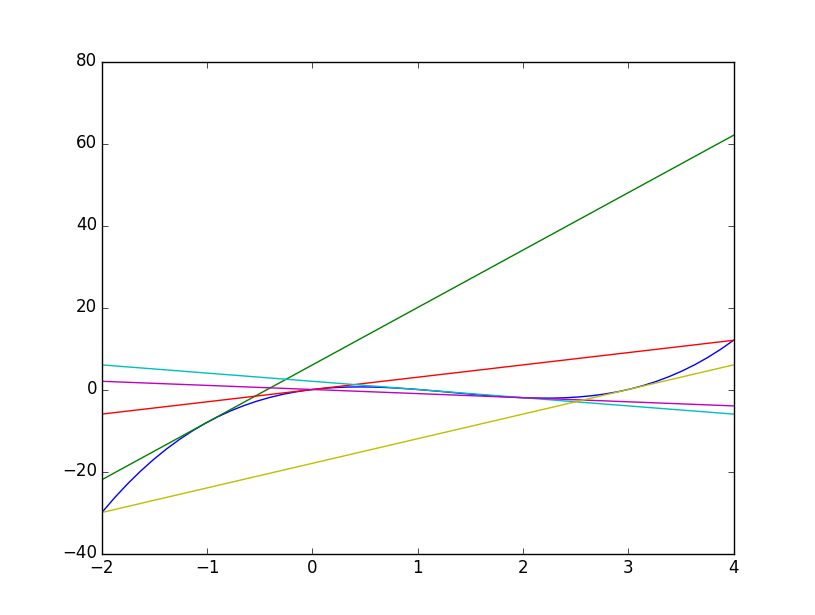
なお、サンプルコードではさらに曲線に対して接線を引いた。f の一次導関数を f.deriv() で得られることを利用する。

#!/usr/bin/env python
"""polynomial.py: Demonstrate how to draw a polynomial curve.
"""
import matplotlib.pyplot as plt
from numpy import (linspace, poly1d)

cur_fig = plt.figure()
cur_axes = cur_fig.add_subplot(111)

# pylint: disable=invalid-name
# Let f be the polynomial whose roots are 0, 1, and 3.
f = poly1d([1, -4, 3, 0])
x = linspace(-2, 4, 50)

# Draw the curve of y = f(x).
cur_axes.plot(x, f(x))

# Draw tangent lines at x = -1, 0, .., 3.
slope = f.deriv()
for i in range(-1, 4):
    cur_axes.plot(x, slope(i) * (x - i) + f(i))

plt.show()

描画結果は次のようなものとなる。

多項式をプロット

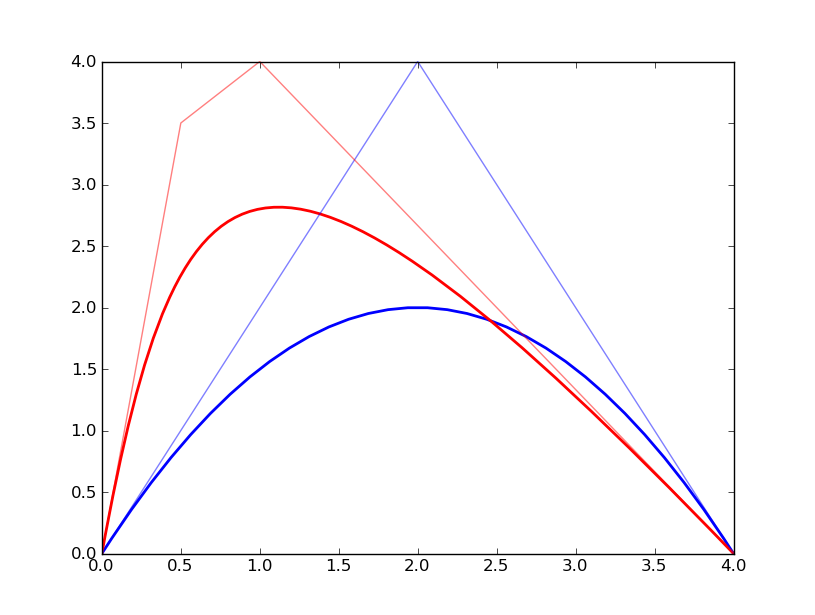
Bézier 曲線

本当は B-Spline 曲線を描画したいのだが、調べてみると Matplotlib では Bézier 曲線が限界のようだ。

手順はこういう感じのようだ：

  1. クラス matplotlib.path.Path のオブジェクトを作成する。この引数として、Bézier 曲線の制御点リストと「打点命令」のリストを渡す。

  2. そのパスオブジェクトを引数として、クラス matplotlib.patches.PathPatch のオブジェクトを作成する。

  3. そのパッチオブジェクトを対象の axes オブジェクトに add_patch する。

Matplotlib は制御点列を与えて Bézier 曲線を定義する流儀のようだ。

まずは簡単な例を。最小の手間で二次の Bézier 曲線（単なる放物線）を定義することを考える。CURVE3 というタイプの曲線は、制御点を三つ与えることで二次の Bézier 曲線を表現できる。CURVE3 ベースの Bézier 曲線の特徴は次のとおり：

  • 最初と最後の制御点は、放物線の始点と終点にそれぞれ一致する。

  • 中間の制御点は、放物線の両端点それぞれの接線の交点と一致する。

  • よって、出来上がりの曲線形状が把握できる。

Path オブジェクト構築は次のようになる：

#!/usr/bin/env python
"""bezier.py: Demonstrate how to draw Bezier curves.
"""
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.path import Path
import matplotlib.patches as patches
import numpy as np

# Unset the face color.
mpl.rcParams['patch.facecolor'] = 'none'

fig = plt.figure()
ax1 = fig.add_subplot(111)

# Define a quadric Bezier curve as path1.
verts1 = np.array([[0., 0.], [2., 4.], [4., 0.]])
codes1 = [Path.MOVETO, Path.CURVE3, Path.CURVE3]

path1 = Path(verts1, codes1)
patch1 = patches.PathPatch(path1, edgecolor='blue', lw=2, alpha=0.5)
ax1.add_patch(patch1)
ax1.plot(verts1[:, 0], verts1[:, 1], color='blue', alpha=0.5)

# Define a cubic Bezier curve as path2.

もうひとつ例を。ドロー系アプリでもよく見かける 3 次の Bézier 曲線を定義する。

  • CURVE4 命令で制御点を指示する。

  • 最初と最後の制御点は、曲線の始点と終点にそれぞれ一致する。

  • 最初の制御点とその次の制御点を結ぶ直線が、曲線の始点での接線に一致する。また、最後の制御点とその前の制御点を結ぶ直線が、曲線の終点での接線に一致する。

  • 曲線全体は、制御点列からなる多角形の内部に位置する。

Path オブジェクト構築は次のようになる：

codes2 = [Path.MOVETO, Path.CURVE4, Path.CURVE4, Path.CURVE4,]

path2 = Path(verts2, codes2)
patch2 = patches.PathPatch(path2, edgecolor='red', lw=2, alpha=0.5)
ax1.add_patch(patch2)
ax1.plot(verts2[:, 0], verts2[:, 1], color='red', alpha=0.5)

ax1.set_xlim(0., 4.)
ax1.set_ylim(0., 4.)

plt.show()

最終的な描画結果は次のようなものとなる：

Bézier 曲線をプロット