チュートリアルを読む

本稿は SymPy の SymPy Tutorial を読んだときのメモである。

Preliminaries

読者は Python プログラミングの基本と、それなりの数学の知識があればよい。チュートリアルに出てくる例はだいたい微分積分レベル。

Installtion

私はインストールは無事に出来たので、ここは読み飛ばした。

• ドキュメント内の至る所にサンプルコードがあり、Sphinx の拡張機能で SymPy Live shell が試せる。よく出来ている。

  • デフォルトの出力書式が LaTeX なので見栄えがする。

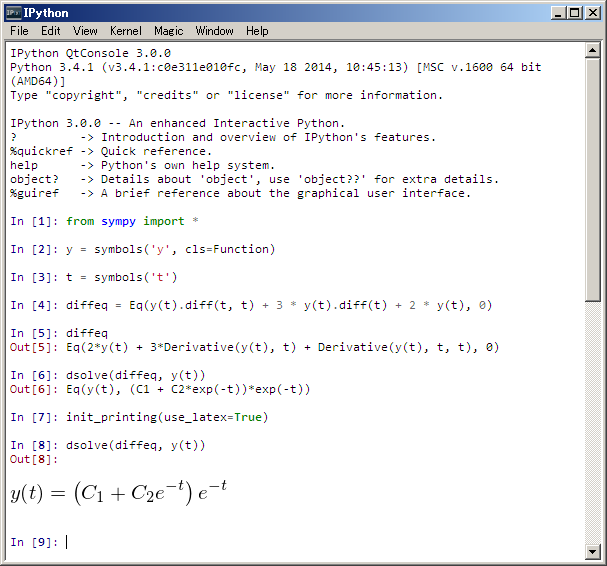
• 最初のサンプル、私の IPython シェルで実行したら次のようになった。若干異なる。おそらく関数 init_printing を異なる引数で適用したか、利用するコンソール環境の Unicode サポート状況に違いがあるのだろう。

  In [1]: a = Integral(cos(x) * exp(x), x)
  
  In [2]: Eq(a, a.doit())
  Out[2]:
    /
   |                 x           x
   |  x             e *sin(x)   e *cos(x)
   | e *cos(x) dx = --------- + ---------
   |                    2           2
  /
  

  以下追記。起動直後に init_printing(pretty_print=False) を呼び出すか、または起動時にコマンドラインオプション --pretty=no とすれば、出力の書式がコンソールにやさしいものに変わる。

  In [3]: init_printing(pretty_print=False)
  
  In [4]: Eq(a, a.doit())
  Out[4]: Eq(Integral(exp(x)*cos(x), x), exp(x)*sin(x)/2 + exp(x)*cos(x)/2)
  

Exercises

• このチュートリアルの基となっている <the 2013 SciPy conference in Austin, TX> とやらを後でチェックしたい。

  • HTML 版はほとんどこのチュートリアルと同じ内容だった。

  • YouTube にビデオ版が公開されている。Part 5 of 6 がおもしろかった。

About This Tutorial

• このチュートリアルは SymPy の機能をたくさん紹介するが、余すところなくというほどではない。

• 紹介している機能についても、その全てのオプションや性能を説明しているとは限らない。

• 全部見たければ API リファレンスを当たればよい。

• <These are the goals of this tutorial> の内容がすばらしい。特に後半。

  • 良い実践、用法を使い、アンチパターンを避けること。

  • 一貫性を保つこと。

  • 不必要な重複を避けること。

Introduction

What is Symbolic Computation?

• 以下、symbolic computation を記号計算と訳しておく。

• 数学オブジェクトを近似ではなく、厳密に表現する。

  • （例）関数 sympy.sqrt と math.sqrt の違い。

  • さらに sympy.sqrt(9) と sympy.sqrt(8) の違いについて。

A More Interesting Example

• 上で見たように、SymPy を用いて無理数を操作できる。

• 記号計算システムは「変数のある記号式の計算」機能を有する。変な訳だ。

• x や y など、記号の定義をするには関数 symbols を用いる。

  • 記号は参照する前に定義しなければならない。Python だから。

  • 式 x + 2 * y は x + 2 y とは書けない。Python だから。

• 本ノートでは simplify を簡略化と訳すことにする。

• 大部分の簡略化は自動的にはなされない。

• まずは関数 expand と factor を試す。

The Power of Symbolic Computation

• 記号計算システムの本来の力は、あらゆる種類の計算を記号的に行うことにある。

• SymPy は次のことができる。すべてを記号的に計算する。

  • 式を簡略化する

  • 微分を計算する

  • 積分を計算する

  • 極限を求める

  • 方程式を解く

  • 行列を用いる

  • and more

• SymPy は次の機能のためのモジュールからなる。

  • プロット

  • 出力（数式をアスキーアートで表現したり LaTeX 記法で表記したり）

  • コード生成

  • 物理学

  • 統計学

  • 組合せ論（この日本語何とかならないか）

  • 数論

  • 幾何学

  • 論理学

  • and more

• init_printing(use_unicode=True) を私のコンソールで実行したら、豆腐系の文字化けが発生した。

• 関数 latex で式の LaTeX コードを出力する。これはたいへん便利なので多用したい。

Why SymPy?

CAS としての SymPy の利点を三つ挙げる。

1. 完全フリー（自由・無料）である。

2. Python を利用する。Python で実行できる。

3. SymPy をライブラリーとして利用できる。

Gotchas

• SymPy は Python ライブラリーであるので、Python から来る制限は SymPy でも引き継がれる。

  • さっきも書いたが、例えば Mathematica みたいに 3 x と書いてしまうのはダメ。

Symbols

• さっきも書いたが、いきなり x は使えない。関数 symbols を呼び出してシンボルオブジェクトを生成する必要がある。

  • この際可能な限り Python の変数と SymPy シンボルとを同じ名前に割り当てるようにする。この例では x = symbols('x') のようにする。

  • 呼び出し symbols('x y z') で三つのシンボルを一度に生成できる。

• 式中のシンボルに値を代入（代入にも置換にも解釈できるのがミソ）するにはメソッド subs を用いる。

Equals signs

• クラス Eq のオブジェクトは方程式を表現する。

  • Eq(lhs, rhs) で lhs == rhs を表現する方程式オブジェクトとなるわけだ。

  • 単に lhs == rhs とすると、両辺が構造的に一致していれば True が得られる。

• 関数 simplify で引数の数式を簡略化する。

  • 詳しい説明は後述するらしい。

  • おそらく、式に含まれるシンボルの量をなるべく少なくするような式変形をするのだろう。

• メソッド equals で式同士が同値かテストする。

Two Final Notes: ^ and /

• 演算子 ^ は Python の規約に従い排他的論理和とする。

  • Xor という型のオブジェクトになるらしい。

• 二項演算子 / の int 型値への適用は Python のバージョンにより整数除算か浮動小数点除算のどちらかになる。

  • 私は Python 3 を使うので、常に浮動小数点型の値を商として得る。

• クラス Integer は整数を表現する。

  • Integer(a)/Integer(b) は Integer(a) が Integer(b) の倍数でなければ Rational 型オブジェクトとなる。

Basic Operations

Substitution

• 式 expr 内のシンボル x に式 y を代入する操作は expr.subs(x, y) のように書く。

• 代入機能を利用する理由はふつうは次のうちのどれかである。

  1. 式をある値で評価するとき

  2. 式の部分に別の式を代入するようなとき

  式の簡略化や展開には微妙なケースがあるらしく、例えばある数式の特定の項だけを展開したいような場合は subs がうってつけらしい。

• メソッド subs は元の式を壊さない。そもそも SymPy の式オブジェクトは immutable である。

• 多変数の同時代入例

  In [1]: expr = x**3 + 4*x*y - z
  
  In [2]: expr.subs([(x, 2), (y, 4), (z, 0)])
  Out[2]: 40
  

Converting Strings to SymPy Expressions

• 関数 sympify と simplify は違う。前者は文字列を SymPy の式にする関数。

  • 内部で Python の eval を呼び出すので危ないとのこと。

  • とは言え、数式の LaTeX 記法を手っ取り早く得る手段として有力のように思う。

• メソッド evalf で式全体を数値的に評価する。e.g. sqrt(8).evalf()

  • 引数で精度を指定できる。任意精度なのですごい。

  • キーワード引数 chop で丸め誤差を削れる。chop=True とする。

• 多数の値で評価するような場合は効率の観点から lambdify の出番。 lambdify(x, expr, "numpy")(a), a = array()

  • numpy.sin を利用するという意味か？

  • 自作関数を利用する方法も提供しているが、これ使うか？

Printing

ところで pretty print を日本語でどう表現するのがよいだろうか。

Printers

SymPy は数式をさまざまなフォームで出力するように制御できる。

str	print による出力形式
repr	式を厳密な表現で出力する
ASCII pretty printer	アスキーアート
Unicode pretty printer	豆腐
LaTeX	標準的な数式の記法
MathML	XML による
Dot	Graphviz 向け

Setting up Pretty Printing

• 関数 init_printing を引数なしで呼び出して、出力制御を初期化する。

  • 関数 init_session が init_printing を内部で呼び出す。

• ipython qtconsole かつ LaTeX がインストール済みならば、 LaTeX を使用する printer を採用する。

  • conda install qtconsole で調達可能。同時に Jupyter のコアパッケージもインストールされる。

  • 以前は --pylab=inline のようなコマンドラインオプションも書いていたと記憶しているが、現在では deprecated である。

  • 出来た！

    

  • Matplotlib がインストール済みでも OK とのこと。

  • IPython notebook では MathJax を使って LaTeX を描画する。

• IPython もしくは Python セッションでは Unicode 出力。ターミナルによる。私のコンソールは豆腐になる。

  • 豆腐が嫌なら init_printing(use_unicode=False) する。

Printing Functions

• ユーザーが出力関数を明示的に指示することが可能。

  • str(expr) と print(expr) の見てくれは同じ。

  • 関数 srepr(expr): expr の「厳密な」表現。

  • 関数 pprint(): ASCII; Unicode をサポートしないターミナルでのデフォルト。

• 関数 pretty

  • pretty(expr, use_unicode=False): string form

  • pretty(expr, use_unicode=True): Unicode form

• 関数 latex(expr) で LaTex form にする。

• MathML は少し面倒。関数 print_mathml がサブモジュール sympy.printing.mathml にある。

• Graphviz 用の dotprint(expr) もある。

Simplification

simplify

• 関数 simplify は数式をもっとも単純な形になるようにがんばる。

  • ただ単によくある単純化操作を適用するだけなので、思うような結果にならないこともある。

  • ムダに遅い。

  • ヒューリスティック。

  • 対話的に利用するのがよいだろう。

Polynomial/Rational Function Simplification

• 関数 expand

  • 単項式の和の canonical form への展開。何？

  • 名前からは簡略化をするものという印象はないし、実際大きくなる。しかし、しばしば式内の項同士でキャンセルが起こって小さくなる。よって、本関数を簡略化関数とみなすことがある。

• 関数 factor

  • 多項式の因数分解。有理数上での規約多項式の積の形に分解する。

  • 多変数も OK だ。

• 関数 factor_list は因数分解の結果をリストで返す。

• 関数 collect

  • 同類項をまとめる。

  • expr.coeff(x, 2): 式 expr の x**2 の係数を返す。

• 関数 cancel

  • 有理関数の約分。分子分母を共通因数のない多項式同士にする。

  • 関数 factor でも cancel できるが、式がすでに約分されているものかどうかを確認することだけ知りたければ cancel のほうがよい。

• 関数 apart

  • 部分分数分解。

  • 本文のサンプルは pritty print の表示がズレていて読みづらい。

Trigonometric Simplification

三角関数編。

• SymPy 版の三角関数と逆三角関数の名前は Python 版の対応するものに準拠する。

• 関数 trigsimp

  • 関数 simplify の三角関数版。三角関数の恒等式に対して適用するのに向いている？

  • 双曲線関数も OK だ。

  • 例によってヒューリスティック。

• 関数 expand_trig

  • 三角関数の加法定理や倍角の公式を展開する場合に使える。e.g. expand_trig(sin(x + y))

Powers

べき乗・指数編。

• 本節冒頭にある指数演算法則の説明が初心を思い出させる。Sufficient conditions to hold は意外に頭にない。

• デフォルトでは SymPy はシンボルを複素数の元とみなすことが判明。

  • それを回避したければ symbols 呼び出し時にキーワード引数を適宜指定。

    • positive=True と real=True を例示。

ここではシンボル x と y を正の実数とし、シンボル a と b を実数とする。

• 関数 powsimp

  • x**a * x**b を x ** (a + b) に展開する。

  • x**a * y**a を (x * y) ** a に展開する。

• 関数 expand_power_exp は x ** (a + b) を x**a * x**b に展開する。

• 関数 expand_power_base は (x * y) ** a を x**a * y**a に展開する。

• 関数 powdenest は (x**a)**b) を x ** (a*b) に展開する。

• どの関数にもキーワード引数 force がある。シンボルが複素数でもムリヤリ展開するようだ。

Exponentials and logarithms

指数と対数編。

• SymPy が気を利かせて Python では与えていない ln = log のような定義をしている。

• 関数 log の引数は複素数でも当然構わないのだが、最初は面倒だからやめるか？ここで言う positive=True, real=True を暗黙に前提としていることが多いから。

ここではシンボル x と y を正の実数とし、シンボル n を実数とする。

• 関数 expand_log

  • log(x + y) を log(x) + log(y) に展開する。

  • log(x ** n) を n * log(x) に展開する。

• 関数 logcombine

  • 関数 expand_log の逆関数的なはたらきをする。

  • log(x) + log(y) を log(x + y) に展開する。

  • n * log(x) を log(x ** n) に展開する。

• どちらの関数にもキーワード引数 force がある。

Special Functions

SymPy の実装している特別関数のうちのいくつかを紹介している。

• 関数 factorial: n => n!

• 関数 binomial(n, k): 記法はタテ括弧による。

• 関数 gamma(x): ガンマ関数そのもの。

• 関数 hyper

  • これは知らん。Wikipedia のページを見たところ、初めて見る式だらけだ。

• メソッド .rewrite(): 与えた関数で式を書き直す。

  • E.g. tan を sin で書き換える。

  • E.g. factorial を gamma で書き換える。

• 関数 expand_func(expr): 特別関数を恒等式を用いて展開する。

• 関数 hyperexpand: 関数 hyper をもっと標準的な関数で書き換える。

• 関数 combsimp: 組み合わせ関連の式の簡略化。

  • E.g. factorial 式同士の商を単純な式に簡略化する。

  • E.g. binomial 式同士の商を単純な式に簡略化する。

  • E.g. gamma 式同士の積を単純な三角関数の式に簡略化する。

Example: Continued Fractions

連分数の例。英語で continued fractions というのか。

• symbols('a0:5') の記法はおもしろい。

• 連分数を cancel する。

• 関数 apart で部分分数分解しまくり。

Calculus

Derivatives

• 関数 diff

  • E.g. diff(x**4, x, x, x): 三階微分。

  • E.g. diff(x**4, x, 3): 同じ三階微分。

  • E.g. diff(expr, x, y, y, z, z, z, z): 偏微分。

  • E.g. diff(expr, x, y, 2, z, 4): 同じ偏微分。

  • メソッド形式の expr.diff(...) も可。

• クラス Derivative

  • 未評価の微分オブジェクトのためのクラス。

  • あるいは SymPy が微分を求められないような式のためのクラス。

  • メソッド .doit() で関数 diff と同じ結果を得る。

  • 遅延評価に有用。

Integrals

• 関数 integrate

  • 不定積分（原始関数）を得るのにも定積分を得るのにも用いる。

  • （例） integrate(cos(x), x)

  • 定数項は含まないのでユーザーが適宜はからう。

  • 定積分は積分域を指定する。

  • integrate(exp(-x), (x, 0, oo))

    • オブジェクト oo が無限大を表現するシンボルか。

  • E.g. integrate(exp(-x**2 - y**2), (x, -oo, oo), (y, -oo, oo)): 重積分

• クラス Integral

  • 用途は Derivative の積分版といったところ。

  • メソッド .doit() で関数 integrate と同じ結果を得る。

• 最後のほう、何を述べているのかわからない。

Limits

• 関数 limit

  • expr.subs(x, oo) などのようにせず limit(expr, x, oo) とすること

  • E.g. limit(sin(x)/x, x, 0): x が 0 に近づくときの極限。

• クラス Limit

  • 用途は Derivative や Integral の極限版といったところ。

  • メソッド .doit() で関数 limit と同じ結果を得る。

• 右極限、左極限

  • E.g. limit(1/x, x, 0, '+')

  • E.g. limit(1/x, x, 0, '-')

Series Expansion

• メソッド series

  • expr.series(x, x0, n) のようにして、関数 expr のある点 x0 における n 次の級数展開を得る。

    • x0 のデフォルト値は 0 である。Maclaurin 展開。

    • n のデフォルト値は 6 である。

  • 出力に O(x**n) のような項が出てくる。

  • メソッド .removeO() でオーダー項が省略できる。

Finite differences

差分商はわからん。

• 関数 as_finite_diff

  • 任意の Derivative オブジェクトに対して、任意階数の微分値の近似を生成できる。

  • ここの最初の例は「ある関数 f の一次微分」を f(x - 1/2) と f(x + 1/2) で近似している。

  • その次の例は「ある関数 f の二次微分」を定義域内の値 h について、以下の値を用いて近似している：

    • f(-3 * h)

    • f(-h)

    • f(2 * h)

• 関数 finite_diff_weights

  • 各 f(h) の項の係数だけ欲しい場合に用いる。

  • もはや f も h も引数に要求されないことに注意。

• 関数 apply_finite_diff

  • 関数 finite_diff_weights を直に使うのは複雑だし、関数 as_finite_diff を f 的なものに操作するのは柔軟性に欠くようならば、本関数を検討する。

Solvers

方程式を解く。

A Note about Equations

• もう一度言うが SymPy では記号方程式を Eq オブジェクトを用いて表現する。

  • x == y を表現したいならばオブジェクト Eq(x, y) を生成する。

• 関数 solve

  • 方程式を指定した未知数シンボルについて解く。

  • E.g. solve(Eq(x**2, 1), x): プラマイ 1 を根とする x の二次方程式を解く。

  • E.g. solve(x**2 - 1, x): 同上。

Solving Equations Algebraically

• 関数 solve

  • 呼び出しの構文は solve(equations variables)

  • 単一の方程式を解くときは、関数 solve の戻り値は解の list である。

  • 解が見つからない（存在しないとは言っていない）場合、次のどちらかが起こる。

    • 空の list が返る。

    • 例外 NotImplementedError が発生する。

  • solve(f(x, y), [x, y]) の形で連立方程式が解けるかもしれない。

    • 多項方程式の重根の多重度も欲しい場合は、関数 roots を用いる。

Solving Differential Equations

ここの例に出てくるのは常微分方程式。

• 関数 dsolve は微分方程式の解を求める。

  • Function オブジェクトが要る。

    • 関数 symbols でキーワード引数 cls=Function を指定する。

  • dsolve(eq, f(x)) の形。

  • 戻り値は Eq オブジェクトである。解が f(x) = ... の形に解けるとは限らないため。

  • 不定積分のときとは異なり、今度は解に任意定数が出てくる。

Matrices

クラス Matrix のコンストラクターは np.array のそれに似ている。

• ただし単リストを引数とすると、生成する行列は列ベクトルの形になる。

• Matrix のオブジェクトは SymPy の型にしては珍しく mutable である。

• 一応 immutable 版の行列型 ImmutableMatrix も提供している。

Basic Operations

どうも NumPy の array にインターフェイスがよく似ているようだ。

• プロパティー .shape: 行列の寸法。

• メソッド .row(i), および .col(i): 列全体および行全体にアクセス。

• メソッド .row_del(i), .col_del(i): 列全体および行全体を削除。

  • これらは in-place に作用する。

• メソッド .row_insert(i, M), .col_insert(i, M): 列全体および行全体を追加。

  • これらは in-place に作用しない。

Basic Methods

• 加算、乗算は普通に演算子で行える。

  • 二項演算子 + で加算。

  • 二項演算子 * でスカラー倍あるいは行列同士の乗算。

  • 二項演算子 ** でべき乗。逆行列もこの記法で M ** -1 のように表現する。

  • プロパティー .T で転置行列を返す。

Matrix Constructors

これも NumPy のスタイルを踏襲しているように見える。もしかすると逆かもしれない。

• 関数 eye で指定次元の単位行列を生成する。

• 関数 zeros で指定サイズの零行列を生成する。

• 関数 ones で指定サイズの行列を生成する。各成分は 1 である。

• 関数 diag で対角行列を生成する。次のどれかが引数になる。

  • スカラーのみを左上から右下までカンマ区切りで一気に指定する。結果は正方行列になる。

  • スカラーか行列で同様にカンマ区切りで一気に指定する。

Advanced Methods

NumPy にあるものとないものがあるようだ。

• メソッド .det() で行列式の値を返す。

• メソッド .rref() は行列の reduced row echelon form を得る。

  • 戻り値は行列の reduced row echelon form とピボット列の添字の list のペアである。

• メソッド .nullspace() で行列の nullspace を探す。

  • 戻り値はその nullspace を張る列ベクトルの list である。

• メソッド .eigenvals() は行列の固有値を探す。

  • 戻り値はキーと値がそれぞれ固有値と（固有多項式の根としての）多重度の dict である。

• メソッド .eigenvects() は行列の固有ベクトルを探す。

  • 戻り値は中身が次のような造りの tuple の list である。

    1. 固有値

    2. 多重度

    3. 固有ベクトルの list

  • 固有ベクトルの計算はたいていコストがかかるので、固有値だけ欲しい場合は .eigenvals() で済ませるのがよい。

• メソッド .diagonalize() は行列を対角化する。

  • 戻り値は Matrix のペアである。それぞれ M = P * D * (P ** -1) なる P と D である。

• 行列の固有多項式が欲しいだけならばメソッド .charpoly を使う。

  • メソッド .eigenvals() よりも効率が良い。

• SymPy では lambda ではなく lamda とつづる。スペリングをうろ覚えの人のようでみっともないが、仕方がない。

Advanced Expression Manipulation

Understanding Expression Trees

• SymPy は数式を木のように表現する。

  • この木を見るには関数 srepr を用いる。数式の木構造を文字列の形で見られる。

• チュートリアルの図は Graphviz と関数 dotprint を組み合わせて作られた。

  • 木の葉に相当する要素は Symbol や Integer など。

  • それ以外の要素は Add や Mul がある。

• 除算のクラスは SymPy には存在しない。Pow と -1 を組み合わせて表現する。

  • Rational は数同士

• 1 + x を評価すると x + 1 と出力されるのは、SymPy の Add がオペランドを任意の（とはいえ整合性のある）順序に並べることから。

  • Add というよりは、可換則の成り立つ演算の際には、ということ。

Recursing through an Expression Tree

• プロパティー func

  • 式の「先頭」のオブジェクトである。

  • E.g. (x*y).func は Mul オブジェクトである。

  • ふつうは式オブジェクトのクラスと一致する。

  • 一致しない場合もあり得る。

    • E.g. Add(x, x) は実は Mul(2, x) である。

    • SymPy は __new__ を多用していて、別のクラスのコンストラクターが返されることがあり得る。

• プロパティー args

  • 式オブジェクトの（木を逆さに見るときの）トップレベルの引数を指す。

  • E.g. (3*y**2*x).args は (3, x, y**2) である。

• func と args から、元の式が完全に再現できる。

Walking the Tree

ジェネレーター preorder_traversal と postorder_traversal で数式の木構造を走査できる。