Python からはじめる数学入門 読書ノート

Python で数学を「やる」本。標準パッケージに加え、Matplotlib と SymPy を使っていろいろやってみるという趣旨の本。

著者:

Amit Saha

訳者:

黒川 利明

出版社:

オライリー・ジャパン

発行年:

2016 年

ISBN:

978-4-87311-768-3

関連 URL:

書籍詳細

1 章 数を扱う

ウォーミングアップ。

• 分数と複素数は Python 標準で扱える。虚数単位は j または J とする。

• それらのオブジェクトを関数 input で生成することもできる。ただし、文字列を実引数とするコンストラクターの処理が空白文字に不寛容だ：

  In [155]: Fraction(input('Enter a fraction: '))
  Enter a fraction: 1 / 273
  ---------------------------------------------------------------------------
  ValueError                                Traceback (most recent call last)
  <ipython-input-155-a5ccacbc5a9b> in <module>()
  ----> 1 Fraction(input('Enter a fraction: '))
  
  D:\Miniconda3\lib\fractions.py in __new__(cls, numerator, denominator, _normalize)
      136                 if m is None:
      137                     raise ValueError('Invalid literal for Fraction: %r' %
  --> 138                                      numerator)
      139                 numerator = int(m.group('num') or '0')
      140                 denom = m.group('denom')
  
  ValueError: Invalid literal for Fraction: '1 / 273'
  

• 複素数を扱う機能を提供するモジュールとして cmath がある。

  IPython でインポートして dir して、基本的な解析関数、二数の比較用関数、座標系変換関数、定数などが提供されていることを確認した。例えば偏角を得るには関数 cmath.phase を用いるようだ。

  複素数のオブジェクトとしての属性は共役、実部、虚部くらいしかないようだ。

• 二次方程式の判別式を得るための平方根の取り方は、本書では math.sqrt ではなく ** 0.5 を採用している。

2 章 データをグラフで可視化する

早くもプロットを扱う。

• クラス list および tuple の基本。

  • 本書では両者の違いを要素を追加できるかどうかの一点に絞って述べている。

  • 要素の反復を for ループで実行でき、要素そのものだけでなく添字も得る場合には enumerate() 関数を用いることに触れている。

• Matplotlib を使ってプロットする。キャンバスの制御方法。

  • 本書のコードを試すときは IPython で pylab を有効にしておくと手っ取り早い。

  • marker='o' と単に o を指定するときの違い。

  • plot 関数は y 列データだけを指定することも、x 列と y 列の両方を指定することもできる。

  • 複数データセットを一度にプロットできる。こういう場合は legend() を活用する。

  • months = range(1, 13) を引数に 3 回渡すのでプロット時に ValueError を生じる？

  • プロットをインクリメンタルに装飾できることに早く気付きたかった。

• インタラクティブシェルでは pylab を、ふつうのスクリプトでは pyplot を使うのが効率的だ。

• pyplot の savefig で画像をファイルに保存できる。

• パラメーター表示される曲線のプロット（例：万有引力、投射軌跡）。

  • 浮動小数点数版 range がない問題は NumPy で片付けたい。この場合は np.linspace(0, 0.72, 720) だ。

  • サンプルコードを見て思うのだが、本書はリストの内包表現を紹介するべきだった。こちらのほうがわかりやすいだろう：

    x_data = [u * np.cos(theta) * t for t in intervals]
    y_data = [u * np.sin(theta) * t - 0.5 * g * t**2 for t in intervals]
    draw_trajectory(x_data, y_data)
    

  • 投擲問題の複数版、タイトル変更コードが抜けている。

• 章末問題で棒グラフ（ヒストグラムではない）を紹介。これは pyplot ベースのコードなので、あえて IPython で pylab ベースで試す。

  In [236]: steps = (6534, 7000, 8900, 10786, 3467, 11045, 5095)
  
  In [237]: labels = ('Sun', 'Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat')
  
  In [238]: positions = range(1, len(steps)+1)
  
  In [239]: pylab.barh(positions, steps, align='center')
  Out[239]: <BarContainer object of 7 artists>
  
  In [240]: pylab.yticks(positions, labels)
  Out[240]:
  ([<matplotlib.axis.YTick at 0x241d1860358>,
    <matplotlib.axis.YTick at 0x241d1b79c50>,
    <matplotlib.axis.YTick at 0x241d088ea20>,
    <matplotlib.axis.YTick at 0x241d189a898>,
    <matplotlib.axis.YTick at 0x241d189ae80>,
    <matplotlib.axis.YTick at 0x241d1cc0390>,
    <matplotlib.axis.YTick at 0x241d1cc0860>],
   <a list of 7 Text yticklabel objects>)
  
  In [241]: pylab.xlabel('Steps')
  Out[241]: Text(0.5,23.3022,'Steps')
  
  In [242]: pylab.ylabel('Day')
  Out[242]: Text(33.5972,0.5,'Day')
  
  In [243]: pylab.title('Number of steps walked')
  Out[243]: Text(0.5,1,'Number of steps walked')
  
  In [244]: pylab.grid()
  

• 章末問題最後の Fibonacci 数の隣接項の比のプロット、下手にコードを書くとべらぼうに時間がかかって面白いとみた。

  お手本コードを改造して、比も同時に返すようなジェネレーターを書くのが楽だ：

  In [272]: def fibo(n):
       ...:     f1 = f2 = 1
       ...:     yield f1, 0
       ...:     if n == 1: return
       ...:     yield f2, 1
       ...:     if n == 2: return
       ...:     for i in range(3, n + 1):
       ...:         next = f1 + f2
       ...:         yield next, next / f2
       ...:         f1, f2 = f2, next
       ...:
  

See also

• Matplotlib 利用ノート

3 章 データを統計量で記述する

統計。

• 本章では母集団全体の統計量を考慮する。

  • つまり Python 標準の statistics.pvariance() と statistics.pstdev() を使えば、本書の計算と一致する。

• 算術平均、中央値、最頻値等、分散、標準偏差を自分で実装する。クラス collections.Counter の使い方がわかる。

  • 算術平均は自作しなくても statistics.mean() で得られる。

  • 中央値は statistics.median() で得られる。さらにその仲間もいる。

  • 最頻値は statistics.mode() で得られる。本書では collections.Counter.most_common() を利用していて、これはこれでおもしろい。最頻値が複数ある場合に StatisticsError が送出されるのが嫌な場合に有益。

• 図 3-1 (p. 80) のプロットはあやしい。

• あとは Peason 相関、散布図の描き方、CSV ファイルの読み込み方など。

  • 単に相関関係といったら Peason のそれを意味することにする。線形関係の強さを測る指標だ。

  • 相関係数の式 (p. 82) を実現するのに Python 組み込みの zip() と sum() を駆使する。

  • Anscombe のデータセットが散布図の重要性に一定の説得力を持たせている。平均、分散、相関係数がすべて同じであっても、データセットとしてはまったく異なることがふつうだ。

4 章 SymPy で代数と式を計算する

ここから SymPy を利用していく。

• Symbol オブジェクトによる数式表現。

• 数式の変形には factor() や expand() などを用いる。

• 数式を出力する際の関数 pprint() の制御方法。本書では <人が式を紙に書く場合に近い形式で出力> するものだと述べている。

  • init_printing() の order 指定がまったく効かない？

• 数式オブジェクトのメソッド subs() によるシンボルへの値の代入。

  • ここにきてようやく辞書の出番だ。

• 文字列を SymPy の数式オブジェクトにするのには関数 sympify() を利用する。

  • 変換失敗時に送出される例外が SympifyError だ。

  • 中学生の代数の宿題を解くツールとか作れそうだ。

• 方程式を solve() で解く。けっこうな種類の方程式を解くことができる。

  • 脚注でも説明があるように、Windows で p. 115 の方程式の解の辞書オブジェクトを出力すると、ここに載せるのもはばかられるような見苦しい形のアスキーアートが得られる。

• SymPy はプロット機能も提供している。

  • 先述の sympify() と組み合わせるとインタラクティブなプロッターが作れる。

  • 複数プロットを定義するときの、Matplotlib とのやり方の違いに注意。

• 章末問題で不等式や有理式を扱う。

  • 多項式の不等式を解くのには solve_poly_inequality() 関数を使う。解となる集合を範囲のリストの形で返すようだ。

  • 有理式の不等式を解くのには solve_rational_inequality() 関数を使う。

    • すごく使いにくい。分子と分母をそれぞれ Poly オブジェクトとして与えるのが面倒だ。

    • 解となる集合を集合の形で返すようだ。なぜ先ほどと流儀が違うのだ。

  • わけのわからない不等式は solve_univariate_inequality() 関数を使う。名前の示すように一変数専用なのだろう。

  • 章末問題の意図は、上記 3 種類の Adapter パターンを実装した不等式ソルバー関数 isolve() を設計、実装しろということだ。そのためにいくつかの問い合わせ関数が有用だと言っている：

    • is_polynomial()

    • is_rational_function()

See also

• SymPy 利用ノート

5 章 集合と確率を操作する

集合と確率。

• 脚注を見ると訳者は確かな数学的知識の持ち主であることが窺える。

• クラス FiniteSet およびそのメソッドの紹介。

• FiniteSet の直積をとるのが簡単。振り子の周期の例題はなるほどという感じだ。

• 一様分布（自力）。

• 事象同士の確率計算には集合同士の演算が対応する。

• 乱数。Python 標準の関数ももちろん利用できる。

  • 基本的だがさいころは random.randint(1, 6) だ。

• 章末問題にベン図 (matplotlib_venn) がある。あとは大数の法則を検証したり、シャッフルしたり、モンテカルロ法みたいなことをする。

  • ベン図のチャレンジで利用する関数の名が venn2 であるのは、その引数である集合がちょうど二つあることを意味する。

  • 問題が物足りないので venn3 でチャレンジした：

    from random import randint
    data = ((i, randint(0, 1), randint(0, 1), randint(0, 1)) for i in range(500))
    venn3(subsets=[set(i[0] for i in data if i[j]) for j in range(1, 4)],
          set_labels=['Football', 'Baseball', 'Others'])
    plt.show()
    

    結果の一例を次に示す。乱数を使用するので実行するたびに出力は異なるはずだ：

    

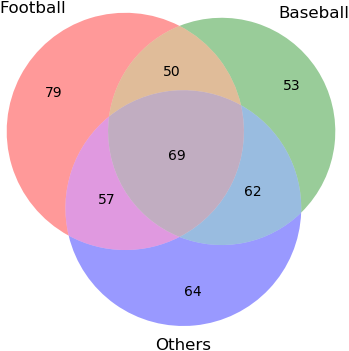
  • 大数の法則のコードは次のようなものだろう：

    from statistics import mean
    
    print('Expected value: 3.5')
    for i in (100, 1000, 10000, 100000, 500000):
        average = mean(randint(1, 6) for _ in range(i))
        print(f'Trials: {i} Trial average {average}')
    

  • カードのシャッフルは私なら次のようにしたい：

    from collections import namedtuple
    from itertools import product
    from random import shuffle
    
    # もしくは enum.Enum
    SUITS = ('spades', 'hearts', 'clubs', 'diamonds')
    RANKS = 'A 2 3 4 5 6 7 8 9 10 J Q K'.split()
    
    Card = namedtuple('Card', ('suit', 'rank'))
    cards = [Card(s, r) for s, r in product(SUITS, RANKS)]
    shuffle(cards)
    

  • 円周率の推定はこう：

    In [96]: def estimate_pi(N):
        ...:     darts = ((uniform(0, 1), uniform(0, 1)) for _ in range(N))
        ...:     dists = (x**2 + y**2 for x, y in darts)
        ...:     hits = len([None for d in dists if d < 1])
        ...:     return 4 * hits / N
        ...:
    
    In [97]: estimate_pi(10000)
    Out[97]: 3.1484
    
    In [98]: estimate_pi(10000)
    Out[98]: 3.1912
    
    In [99]: estimate_pi(10000)
    Out[99]: 3.1636
    
    In [100]: estimate_pi(10000)
    Out[100]: 3.1504
    

6 章 幾何図形とフラクタルを描画する

Matplotlib のより高度な API を利用する。

• Patch と呼ばれる簡単な図形を描画する。

• Animation もサポート。

  • 一時変数が未使用に見えるかもしれないが、早過ぎるガベージコレクションを回避するために必要。

  • このスクリプトを IPython から %run するとアニメーションが効いていない。

  • 投射軌跡のアニメーションは、入力によってはボールの絵の大きさが過剰になることがある。

  • 投射軌跡のアニメーションはボールが縦長で違和感がある。前のコードを参考にして、アスペクト比を揃えるのがいい。

• フラクタル、 ランダムウォーク、 シェルピンスキーギャスケット、 バーンズレイのシダ エノン写像

  • フラクタルの基本としてある種のランダムウォークを挙げている。

  • random.choice で関数呼び出しを振り分けるのはおもしろかった。

  • Barnsley シダの変換 3 は本文テキストとコードとで変換が違う。実行した限りではコードのほうが正。

  • シダの get_index 周辺は自作せずとも Python の random.choices がうまくやってくれる。こんな非一様抽選は昔のドラクエがよく実装していた。

  • シダを描くのもガスケットを描くのも同じロジックというのは衝撃的だ。エノン写像は乱数性がなくなってさらに簡単に描ける。

• マンデルブロ集合 のために imshow を用いる。

  • initialize_image は内包表記をうまく使えば一行コードだ。

    def initialize_image(x_p, y_p):
        return [[0] * x_p for i in range(y_p)]
    

  • abs(z1) < 2 ではなく z1.real**2 + z1.imag**2 < 4 のようにして、少しでも計算時間短縮化を狙うといい。

  • 実際に集合を描画したところ、思いのほか絵がボケていて悲しかった。本文では点の数を増やすことで詳細になるとあるが、ドットが細かくなっただけのような気がした。

7 章 初等解析問題を解く

極限、微分、積分、そしてなぜか確率密度関数を扱う。

• 標準の math パッケージが有用な関数を提供している。

• 極限は SymPy クラス Limit が使える。例題である種の複利計算の極限値を求める。

• 微分は SymPy クラス Derivative が使える。常微分も偏微分も同じインターフェイス。

• 極値の計算には \(f'(x) = 0\) や \(f''(x) = 0\) を solve することが重要だ。

• 勾配上昇法を自力で実装する。このアルゴリズムは初期値の選定がたいへん重要だ。

  • 上昇法と下降法のコードは、点列を生成する部分の符号が入れ替わるだけの違いしかない。

  • 改造版のコードは何らかの例外を送出するべきだと思う。

• 積分は SymPy クラス Integral が使える。原始関数と定積分の両方を求めるのに利用できる。

• 確率密度関数各種。いわゆるグラフの面積が確率の値を意味する。

  • 正規分布を自作しているが、もちろん SymPy も備えている。

    In [62]: from sympy.stats import Normal, density
    
    In [63]: X = Normal('X', 10, 1)
    
    In [64]: (density(X).cdf(12) - density(X).cdf(11)).evalf()
    Out[64]: 0.135905121983278
    

• 章末問題に曲線の長さを求める主題のものがある。図の放物線の与えられた範囲の長さは次のようにして得られた：

  In [91]: from sympy import integrate, diff, sqrt, symbols
  
  In [92]: x = symbols('x')
  
  In [93]: fx = 2 * x**2 + 3 * x + 1
  
  In [94]: integrate(sqrt(1 + diff(fx, x)**2, (x, -5, 10))
  Out[94]: asinh(17)/8 + asinh(43)/8 + 17*sqrt(290)/8 + 215*sqrt(74)/8
  
  In [95]: _.evalf()
  Out[95]: 268.372650946022
  

付録 A ソフトウェアのインストール

Windows だけ読んだ。本書は Anaconda の使用を推奨している。どうもこの記述の内容からすると、Matplotlib も SymPy も勝手にインストールされるようだ。

• ただし明示的にアップグレードする方法があるので、それを紹介している。

• 前述したベン図のパッケージは pip でインストール可能だ。訳者は失敗したらしいが。

  bash$ pip show matplotlib-venn
  Name: matplotlib-venn
  Version: 0.11.5
  Summary: Functions for plotting area-proportional two- and three-way Venn diagrams inmatplotlib.
  Home-page: https://github.com/konstantint/matplotlib-venn
  Author: Konstantin Tretyakov
  Author-email: kt@ut.ee
  License: MIT
  Location: d:\miniconda3\lib\site-packages
  Requires: numpy, matplotlib, scipy
  Required-by:
  

付録 B Python について

• 内包表記は本文中で紹介するべきだった。

• 例外処理の記述量は入門書としては最適と思われる。

あとがき

Project Euler について言及している。

訳者あとがき

Computer Based Math について述べられている。