第 8 章 多様体上のベクトル場(後編)¶
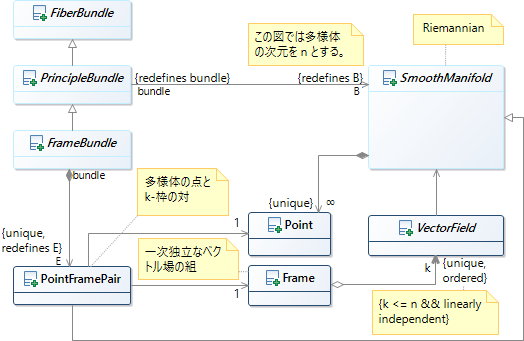
8.4 \(k\)-枠場(展開)¶
- \(k\)-枠場
多様体 \(M\) 上の一次独立なベクトル場 \(k\) 個の組を意味する。\({0 \le k \le \dim M}\)
例:二次元曲面 \({\Sigma_g\ (g \le 2)}\) 上には 1-枠場と 2-枠場のどちらも存在しない。一方、トーラス \(T^2\) 上にはどちらも存在する。
n-枠場を持つ \(n\) 次元多様体を 平行可能化多様体 と呼ぶ。
2-枠場のある多様体 \(M\) 上で \({[\xi_1, \xi_2] = 0}\) であれば \(\RR^2\) の \(M\) への作用 \({(\varphi_1^{t_1} \circ \varphi_2^{t_2})(x)}\) を定義することで \(\RR^2\) 作用の軌道の族で \(M\) を分割することができる。このとき、軌道は \(M\) の各点の近傍に対して二次元の共通部分を持つ。
\({x \in M}\) を固定すると作用の接写像のランクが 2 である。
共通部分は高々可算個である。
これを 2 から \(k\) に拡張する。一般に \(k\)-枠場 \({(\xi_1, \dotsc, \xi_k)}\) が \({[\xi_i, \xi_j] = 0}\) であるならば、加法群 \(\RR^k\) の \(M\) への作用を次のように定義できて、\(M\) は \(k\) 次元の \(\RR^k\) 作用の軌道に分割される。
\(M\) の各点の近傍 \(U\) においてランク \({n - k}\) の写像 \(\fn{F}{U}\RR^{n - k}\) が存在して、軌道と近傍の共通部分が \(F\) で決まる近傍の \(k\) 次元部分多様体の和集合となる。
例 8.4.1: \(\RR^3\) 上のベクトル場
\({f \in C^\infty(\RR^2).}\)
\({\displaystyle \xi_1 = \frac{\partial}{\partial x_1} + \frac{\partial f}{\partial x_1}\frac{\partial}{\partial x_3},}\) \({\displaystyle \xi_2 = \frac{\partial}{\partial x_2} + \frac{\partial f}{\partial x_2}\frac{\partial}{\partial x_3}.}\)
\({[\xi_1, \xi_2] = 0.}\)
\({h = x_3 - f(x_1, f_2)}\) が一定である点からなる曲面が \(\RR^2\) 作用の軌道となる。
例 8.4.2: ダメな例
\({\displaystyle \xi_1 = \frac{\partial}{\partial x_1} - x_2 \frac{\partial}{\partial x_3},}\) \({\displaystyle \xi_2 = \frac{\partial}{\partial x_2}.}\)
\({\because [\xi_1, \xi_2] = \dfrac{\partial}{\partial x_3}.}\)
- k 次元接平面場 or k 次元分布
多様体 \(M\) 上の \(k\) 次元接平面場に対して、各点の近傍ではその \(k\) 次元接平面場を張る \(k\)-枠場に取り替えられる。
定理 8.4.3: \(\RR^n\) の開集合 \(U\) 上の \(k\)-枠場が \(U\) の各点の近傍に対して \({[\xi_i, \xi_j]}\) が 0 となる \(k\)-枠場に取り替えられることは、\({[\xi_i, \xi_j]}\) が \(\xi_1, \dotsc, \xi_k\) の張る \(k\)-枠場に値を持つことと同値である。
証明がよくわからない。
\({(\xi_1, \dotsc, \xi_k)}\) と \({(\eta_1, \dotsc, \eta_k)}\) が同じ接平面場を与えるならば \({\exists \fn{a_{ij}}{U}GL_k(\RR)\quad\text{s.t. } \eta_i = \sum_{j = 1}^k a_{ij}\xi_j}\) を示す。
一方の括弧積を計算することで、他方の括弧積と同時に接平面場に値を持つことがわかる:
\[\begin{split}\begin{align*} [\eta_l, \eta_m] &= \left[\sum_{i = 1}^k a_{li}\xi_i, \sum_{k = 1}^k a_{mi}\xi_i\right]\\ &= \sum_{i, j} a_{li}\xi_j(a_{mj})\xi_j - \sum_{i,j} a_{mj}(\xi_j a_{li})\xi_i + \sum_{i,j}a_{li}a_{mj}[\xi_i, \xi_j]. \end{align*}\end{split}\]
十分:適当に座標を取り替えて写像 \(\fn{p}{\RR^n}\RR^k\) を \({p(\bm x) = (x_1, \dotsc, x_k)}\) で定義する。
点の近傍上 \(p_*\) を接平面場に制限した接写像は何かとの同型を与える。
その次の「\(V\) 上の k 枠場 \({(\eta_1, \dotsc, \eta_k)}\) を \({p_* \eta_i = \dfrac{\partial}{\partial x_i}}\) となるようにとれる」がわかりにくい。
\({[\eta_l, \eta_m]}\) が値を持てば \({p_*[\eta_l, \eta_m] = \left[\dfrac{\partial}{\partial x_i}, \dfrac{\partial}{\partial x_j}\right] = 0}\) より 0 が値である。
フローの可換性の成立だけで \(U\) 内の「軌道」が \(F\) によって定まる \(U\) の \(k\) 次元部分多様体となるといえる。
「軌道」と書いたが、\(x\) において \(k\) 次元接平面場は \({T_x(F\inv(F(x)))}\) と一致する。
定理 8.4.4: フロベニウス
\({[\xi_i, \xi_j]}\) が \(k\) 次元接平面場に値を持つということを (完全)積分可能条件 という。
\({F_V\inv(F_V(x)),\ T_x(F_V\inv(F_V(x))) \subset T_xM}\) と \(x\) における \(k\) 次元接平面場が一致する。
(極大)積分多様体 or 葉
共通部分できれいに貼り合わさる。
「正則とは限らない」部分多様体とは?
葉層 構造(本書図 8.2 参照)
8.5 勾配ベクトル場¶
多様体上の微分可能関数 \({f \in C^1(M)}\) とベクトル場 \(X\) とリーマン計量 \(g\) に対して、ベクトル場 \(\grad f\) を次で定義する:
\(f\) の等位面が部分多様体であるとき、\(f\inv(a)\) と \(\grad f\) は直交する。なぜならば \(f\inv(a)\) の接ベクトル \(v\) を取ると \({f_*v = 0}\) であって \({g(v, \grad f) = 0}\) が成り立つ。
\[f_*v = 0 \implies g(v, \grad f) = \sum \frac{\partial}{\partial x_i} v_i = 0\]\(\grad f\) が生成するフローを gradient flow と呼ぶ。
例 8.5.1: 球面上の微分可能関数に対する勾配ベクトル場
\(S^2\) のパラメーター表示を \({(x, y, z) = (\cos\theta\cos\cos\varphi, \sin\theta\cos\varphi, \sin\varphi)}\) とおく。
ベクトル場の基底を \({\dfrac{\partial}{\partial \theta}, \dfrac{\partial}{\partial \varphi}}\) ととる。
リーマン計量は \({\displaystyle g = \begin{pmatrix}\cos^2\varphi & 0\\0 & 1\end{pmatrix}}\) と書ける。
次のようにおいて \({g(\grad f, X)}\) と \(X(f)\) をそれぞれ計算する:
\[\begin{split}\begin{align*} \grad f &= a\frac{\partial}{\partial \theta} + b\frac{\partial}{\partial \varphi},\\ X &= u\frac{\partial}{\partial \theta} + v\frac{\partial}{\partial \varphi}. \end{align*}\end{split}\]計算の結果 \({\grad f = \cos\varphi \dfrac{\partial}{\partial \varphi}}\) となる。直交座標系で書くと \({-xz\dfrac{\partial}{\partial x} - yz\dfrac{\partial}{\partial y} + (1 - z^2)\dfrac{\partial}{\partial z}.}\)
例題 8.5.2
\({f(x, y) = x^3 - x + y^2}\) のグラフを描け。
フローが等位線と直交するように描くのが鉄則。
\({X = \dfrac{\partial f}{\partial x}\dfrac{\partial}{\partial x} + \dfrac{\partial f}{\partial y}\dfrac{\partial}{\partial y}}\) はユークリッド計量についての \(f\) の勾配ベクトル場である。
\({Xf = \left(\dfrac{\partial f}{\partial x}\right)^2 + \left(\dfrac{\partial f}{\partial y}\right)^2 \le 0}\) より非減少である。
\({\displaystyle \diff{x}{t} = \frac{\partial}{\partial x}, \ \diff{y}{t} = \frac{\partial}{\partial y}}\) の解曲線を求めろ。
問題 8.5.3
\({\grad f \ne 0}\) なる点で定義されるベクトル場 \({\displaystyle Y = \frac{\grad f}{g(\grad f, \grad f)}}\) およびその解曲線 \(c(t)\) について。
定義域では \({f(c(t_0 + t)) - f(c(t_0)) = t.}\) \({Yf = 1}\) より \({\displaystyle \diff{(f \circ \varphi_t)(x)}{t} = (Yf)(\varphi_t(x)) = 1.}\) \({\therefore\ f(\varphi_t(x)) - f(x) = t.}\)
モース関数について
臨界点近傍で \({\displaystyle f = \sum_{i = 1}^\lambda x_i^2 + \sum_{i = \lambda + 1}^n x_i^2.}\)
1 の分割の技法を使ってリーマン計量 \(g\) を \({g_{ij} = \delta_{ij}}\) となるように定める。このとき勾配ベクトルは次のようになる:
\[\grad f = -2 \sum_{i = 1}^\lambda x_i \frac{\partial}{\partial x_i} + 2 \sum_{i = \lambda + 1}^n x_i\frac{\partial}{\partial x_i}.\]解曲線は \({(\mathrm e^{-2t}x_1, \dotsc, \mathrm e^{-2t}x_{\lambda}, \mathrm e^{2t}x_{\lambda + 1}, \dotsc, \mathrm e^{2t}x_n).}\)
\({f\inv(x^0 - \eps)}\) と \({f\inv(x^0 + \eps)}\) の間には二枚の平面を除いて対応が付いている。
例 8.5.4: トーラス \({f(x, y) = a(2 + \cos y)\cos x + c \sin y}\)
\(\RR^3\) 内のトーラス (p. 24) として考える。
\({\displaystyle Df = \begin{pmatrix}-a(2 + \cos y)\sin x & -a \sin y\cos x + a \cos y\end{pmatrix}.}\)
\({\displaystyle g = \begin{pmatrix}(2 + \cos y)^2 & 0\\0 & 1\end{pmatrix}.}\) (cf. 例題 7.1.4)
\({\displaystyle g\inv = \begin{pmatrix}\dfrac{1}{(2 + \cos y)^2} & 0\\0 & 1\end{pmatrix}.}\)
定義に従って勾配ベクトル場を計算するのは容易い:
\[\grad f = -\frac{a\sin x}{2 + \cos y}\frac{\partial}{\partial x} + (-a \sin y\cos x + c\cos y)\frac{\partial}{\partial y}.\]
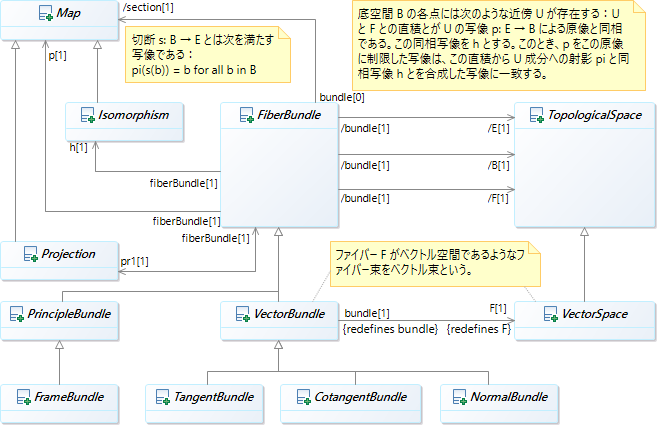
8.6 ファイバー束(展開)¶
ここでファイバー束およびそれに関係する簡単な概念のいくつかを図式化したものを次に示す。
例題 8.6.1: ファイブレーション定理
\(M, N\) をコンパクト連結多様体で \({\dim M \gt \dim N}\) であり、
\({F \in C^\infty(M, N)}\) が
\({\forall x \in M, \fn{F_*}{T_xM}T_{F(x)}N}\) が全射である
とする。このとき \({\forall y \in N}\) に次のような近傍 \({V_y \owns y}\) と同相写像 \(h\) が存在する:
\(\fn{h}{F\inv(V_y)}V_y \times F\inv(y),\)
\({F = \operatorname{pr}_1 \circ h,}\)
\(\operatorname{pr_1}\) は第一成分への射影。
証明:
リーマン計量を \(g\) とする。
接空間の部分集合 \({\nu_x = \set{v \in T_x(M) \sth \forall w \in T_x(F\inv(F(x))), g(v, w) = 0}}\) を定義する。
\({F_*|\nu_x}\) が同型写像になるという性質がある。
ある一点 \({y^0 \in N}\) の開被覆として \({(V, \psi = (y_1, \dotsc, y_n)),\ \psi(y^0) = (0, \dotsc, 0)}\) をとる。
近傍 \({W \owns y^0}\) を \({\closure{W} \subset V}\) となるようにとる。
\(C^\infty\) 級関数 \(\fn{\mu}{N}\RR\) を次のように定義する:
\({\supp \mu = V,}\)
\({y \in \closure{W} \implies \mu(y) = 1.}\)
\(N\) 上の \(C^\infty\) 級ベクトル場 \({\xi_i = \mu\dfrac{\partial}{\partial y_i}}\) を考える。
また \({\bm a \in \RR^n}\) として \({\xi_{\bm a} = \sum_{i = 1}^n a_i\xi_i}\) およびそれが生成するフロー \({\varPsi_{\bm a}^t}\) を考える。
これはある \({\eps \gt 0}\) について次のような性質がある:
\[t\norm{\bm a} < \eps \implies \varPsi_{\bm a}^t(y^0) = \psi\inv(t\bm a).\]\({F_*|\nu_x}\) は同型なので \(\xi_i\) に対して \(M\) 上のベクトル場 \({\overset{\sim}{\xi_i}}\) を次が成り立つように一意的に取れる:
\[F_* \overset{\sim}{\xi_i} = \xi_i, \ \overset{\sim}{\xi_i}(x) \in \nu_x.\]この状況をファイバー束の接続という。
\({\overset{\sim}{\xi_i}}\) を \(\xi_i\) の 持ち上げ という。
\({\displaystyle \overset{\sim}{\xi}_{\bm a} = \sum_{i = 1}^n a_i \overset{\sim}{\xi_i}}\) とおくと \({F_* \overset{\sim}{\xi}_{\bm a} = \overset{\sim}{\xi}_{\bm a}.}\)
ゆえに 例題 6.5.5 のベクトル場の射影の性質により、 \({\overset{\sim}{\xi}_{\bm a}}\) のフロー \({\varPhi_{\bm a}^t}\) について次が成り立つ:
\[F \circ \varPhi_{\bm a}^t = \varPsi_{\bm a}^t \circ F.\]写像 \({\fn{H}{\set{\bm a \in \RR^n \sth \norm{\bm a} \lt \eps} \times F\inv(y^0)}M}\) を \({H(\bm a, x) = \varPhi_{\bm a}^1(x)}\) で定義する。
注意 6.3.6 より \(H\) は \(C^\infty\) 級である。
\({F(H(\bm a, x)) = \varPsi_{\bm a}^1(F(x)) = \varPsi_{\bm a}^1(y^0) = \psi\inv(a).}\)
\(H\) の逆写像は \({x \longmapsto (\psi(F(x)), \varPhi_{\psi(F(x))}(x))}\) で与えられる。
よって写像 \(H\) は微分同相写像である。
- ファイバー束
位相空間 \(E, B\) と連続写像 \(\fn{p}{E}B\) について次が成り立つ位相空間 \(F\) が存在すれば、これを ファイバー といい、\(p\) をファイバー束という:
\[\forall b \in B, \exists U_b \owns b \quad \text{ s.t. } \exists \fn{h}{p\inv(U_b)}U_b \times F,\ \operatorname{pr}_1 \circ h = p.\]- 平坦な接続
例題 8.6.1 における \({[\overset{\sim}{\xi}, \overset{\sim}{\eta}]}\) を考える。
持ち上げによってベクトル場 \({[\overset{\sim}{\xi}, \overset{\sim}{\eta}]}\) は \({F_*[\overset{\sim}{\xi}, \overset{\sim}{\eta}] = [F_*\overset{\sim}{\xi}, F_*\overset{\sim}{\eta}] = [\xi, \eta].}\)
最初と最後の等号はそれぞれ 例題 8.2.3 と持ち上げによる。
特に座標近傍上で \({\displaystyle \xi = \zeta_i = \frac{\partial}{\partial x_i}}\) をとれば、\({[\zeta_i, \zeta_j] = 0}\) なので \({[\overset{\sim}{\zeta_i}, \overset{\sim}{\zeta_j}]}\) はファイバーの方向のベクトル場である。
さらに \({\forall \zeta_i, \zeta_j,\ [\overset{\sim}{\zeta_i}, \overset{\sim}{\zeta_j}] = 0}\) のときには接続が平坦な接続であるという。
各 \(\zeta_i\) が生成するフローを \(\varphi_i^{t_i}\) とすると、各フローは局所的には可換である。
\({x \in M}\) と 0 近傍の点 \({(t_1, \dotsc, t_n)}\) に対し、 \({\varPhi(t_1, \dotsc, t_n)(x) = \varphi_1^{t_1} \circ \dotsb \circ \varphi_n^{t_n}(x)}\) とおく。
\({\psi(F(\varPhi(t_1, \dotsc, t_n)))(x) = \psi(F(x)) + (t_1, \dotsc, t_n),}\)
\({\varPhi(s_1, \dotsc, s_n) \circ \varPhi(t_1, \dotsc, t_n)(x) = \varPhi(s_1 + t_1, \dotsc, s_n + t_n)(x).}\)
微分同相写像 \({x \longmapsto (F(x), \varPhi(\psi(y) - \psi(F(x)))(x))}\) に関する \({U_y \times \set{z}}\) の逆像は部分多様体のように貼り合わされる。
ファイバーがリー群であるようなファイバー束を考えることができる。
\(G\) がファイバーを左または右から \(M\) に作用している。
この作用について不変なファイバーに対して横断的な接平面場を考えると、持ち上げが \(G\) の作用で不変となるような接続がある。このとき \({[\overset{\sim}{\xi}, \overset{\sim}{\eta}]}\) も不変ベクトル場であり、\(G\) のリー代数 \(\mathfrak g\) の元である。
\(n\) 次元リーマン多様体の \(\operatorname{Fr}M\) はファイバーが \(O(n)\) であるような \(M\) 上のファイバー束となっている。
レビチビタ接続 とはこのファイバー束の接続である。
8.7 第 8 章の問題の回答¶
ノートは以上に記した。