第 3 章 微分形式の積分 1/3¶
コンパクト多様体 \(M\) の \(\H^p(M)\) が有限次元であるならば:
\[\dd \alpha = 0 \quad\text{and } \H^p(M) \owns [\alpha] = 0 \iff \exists \beta \in \varOmega^{p - 1}(M) \quad\text{s.t. } \dd \beta = \alpha.\]\(\H^p(M)\) が自明でないときには、今のところは自力で判定するしかない。マイヤー・ビエトリス完全系列やチェック・ドラーム完全系列を調べることになる。
\({[\alpha] = 0}\) であるかどうかは、有限個の積分により判定が可能となる。
3.1 閉微分 1 形式の積分¶
連結多様体 \(M\) 上の曲線 \(\fn{\gamma_x}{[0, 1]}\RR\) 上で積分を定義する。
これは \({x_0, x \in M}\) を結ぶ曲線であり、\({\gamma_x(0) = x_0}, \ {\gamma_x(1) = x}\) を満たすものとしておく。
関数 \(\fn{f}{M}\RR\) について閉 1 形式 \(\alpha\) を \({\alpha = {\dd f}}\) で定義する。
下の左の二つの意味が同じ積分を、右の二つの意味が同じ積分で定義する:
\[\int_{\gamma_x}\!\alpha = \int_{\gamma_x}\!\dd f = \int_0^1\!\gamma_x^* \alpha = \int_0^1\!\gamma_x^*\,\dd f.\]これの根拠は次の式が成り立つことによる:
\[f(x) - f(x_0) = f(\gamma_x(1)) - f(\gamma_x(0)) = \int_0^1\!\diff{f\circ \gamma_x}{t}\,\dd t.\]積分記号の中身全部は \({\gamma_x \dd f}\) である。これは 定義 2.1.7 と 命題 2.3.6 による。
この閉 1 形式に対して積分の値が経路のとり方に依らなければ、 \({\displaystyle f(x) = \int_{\gamma_x}\!\alpha}\) と定義すれば \({\alpha = \dd f}\) となる。
\({\alpha = \dd f}\) なる \(f\) が存在することと、すべての閉曲線 \(\gamma\) について \(\displaystyle {\int_\gamma\!\alpha = 0}\) であることは同値である。
\({\H^p(M) \owns [\alpha] \ne 0}\) ならば、\(\displaystyle {\int_\gamma\!\alpha \ne 0}\) なる \(f\) が存在する。
例題 3.3.1: 全微分すると与えられた微分形式に一致する関数の存在する十分条件
\(M\) をコンパクト多様体、
\({\H^1(M) \cong \RR^k},\)
次の条件を満たす多様体上の閉曲線 \(\gamma_1, \dotsc, \gamma_k\) が存在する:
\[\int_{\gamma_i}\!\alpha = 0\quad\text{for }i = 1, \dotsc, k.\]
このとき \({\alpha = \dd f}\) を満たす多様体上の関数 \(f\) が存在する。
\(\H^1(M)\) の基底を \([\alpha_1], \dotsc, [\alpha_k]\) とおく。
線形代数の各種命題の証明にありがちなアルゴリズムにより、次の正方行列が正則であるように閉曲線 \(\gamma_1, \dotsc, \gamma_k\) がとれる:
\[\left(\int_{\gamma_j}\!\alpha_i\right)_{i, j = 1, \dotsc, k}.\]閉 1 形式 \(\displaystyle {[\alpha] = \sum_{i = 1}^k b_i [\alpha_i]}\) となるように各 \({b_i \in \RR}\) をとる。
\(\displaystyle {\int_{\gamma_j}\!\alpha = \sum_{i = 1}^k b_i \int_{\gamma_j}\!\alpha_i = 0},\)
\({\det\left(\int_{\gamma_j}\!\alpha_i\right) \ne 0}\)
より、すべての \({b_j = 0}\)
ゆえに \({\int_{\gamma_i}\!\alpha = 0} \implies {\H^1(M) \owns [\alpha] = 0}.\)
前ページの黒丸より \({\alpha = \dd f.}\)
例 3.1.2: トーラス \({T^n = \RR^n/\ZZ^n}\) での事情
\({\H^1(T^n) \cong \RR^n}\) であるので(前章で何度か言及された)基底として \([\dd x_1], \dotsc, [\dd x_n]\) がとれる。
曲線 \(\fnm{\gamma_j}{[0, 1]}{\RR^n}{t}t\bm e_j\) に対して \(\displaystyle {\int_{\gamma_j}\!\dd x_i = \delta_{ji}}\) が成り立つ。右辺はクロネッカーの記号。
閉形式 \({\alpha \in \varOmega^1(T^n)}\) に対して、各曲線に沿う積分がゼロであるならば、\({\alpha = \dd f}\) を満たすトーラス上の関数 \(f\) が存在する。
一般には次を満たす関数 \(f\) が存在する:
\[\alpha - \sum_{i = 1}^n \int_{\gamma_i}\!\alpha \,\dd x_i = \dd f.\]
問題 3.1.3: \(C^\infty\) ホモトピックならば積分値は経路の取り方に依らない
\(C^\infty\) 級関数 \(\fn{F}{{[0, 1]}\times{[0, 1]}}M\) が
\[\begin{split}\begin{align*} F(0, t) &= \gamma_0(t),\quad F(s, 0) = x_0,\\ F(1, t) &= \gamma_1(t),\quad F(s, 1) = x_1 \end{align*}\end{split}\]を満たすとすると、すべての閉 1 形式 \(\alpha\) の経路積分は同じである:
\[\begin{split}\begin{align*} \int_{\gamma_1}\!\alpha - \int_{\gamma_0}\!\alpha &= \int_0^1\!\gamma_1^*\alpha - \int_0^1\!\gamma_0^*\alpha\\ &= \int_{[0, 1]\times\set{0}}\!F^*\alpha + \int_{\set{1}\times[0, 1]}\!F^*\alpha - \int_{[0, 1]\times\set{1}}\!F^*\alpha - \int_{\set{0}\times[0, 1]}\!F^*\alpha\\ &= \int_{[0, 1]\times[0, 1]}\!F^*\,\dd \alpha\\ &= 0. \end{align*}\end{split}\]最初の等号は 1 形式の積分の定義による。本節冒頭参照。
二番目の等号はホモトピックであるという仮定による。
三番目の等号は長方形上の 1 形式に対する積分であることによる。命題 1.3.1 参照。
最後の等号は与えられた微分形式が閉形式であることによる。
3.2 単体からの写像に沿う積分¶
まずは直方体。\(p\) 形式を \(p\) 次元直方体上で積分する。
\(\fn{\kappa}{[a_1, b_1] \times \dotsb \times [a_p, b_p]}M\)
\({\alpha \in \varOmega^p(M)}\)
このとき \({\kappa^*\alpha \in \varOmega^p([a_1, b_1] \times \dotsb \times [a_p, b_p])}.\) \({\kappa^*\alpha = f(t_1, \dotsc, t_p)}\,{\dd t_1 \wedge \dotsb \wedge \dd t_p}\) となる関数 \(f\) が存在するので、直方体上の \(p\) 形式の積分を次で定義する:
次に単体に沿う積分を定義する。
\(p\) 次元標準 単体 を定義する:
\[\Delta^p = \set{(x_1, \dotsc, x_p) \in \RR^p \sth 1 \ge x_1 \ge \dotsb \ge x_p \ge 0}.\]単体からの写像に沿う積分を次で定義する:
\[\int_{\Delta^p}\!f(x_1, \dotsc, x_p)\,\dd t_1 \wedge \dotsb \wedge \dd t_p = \int_{x_1 = 0}^1\dotsi \int_{x_i = 0}^{x_{i - 1}}\dotsi \int_{x_p = 0}^{x_{p - 1}}\! f(x_1, \dotsc, x_p)\,\dd x_p \dots \dd x_i \dots \dd x_1.\]\(C^\infty\) 級写像 \(\fn{\sigma}{\Delta^p}M\) に沿う積分を次で定義する:
\[\int_\sigma\!\alpha = \int_{\Delta^p}\!\sigma^*\alpha.\]写像 \(\sigma\) を \(C^\infty\) 級特異 \(p\) 単体 or \(p\) 次元 \(C^\infty\) 級特異単体という。
特異 \(p\) 単体有限個の形式的な線形結合を \(C^\infty\) 級特異 \(p\) チェイン or \(p\) 次元 \(C^\infty\) 級特異チェインという。
\[\sum_{i = 1}^j a_i \sigma_i, \quad a_i \in \RR.\]
\(C^\infty\) 級特異 \(p\) チェイン上の積分を次で定義する:
\[\int_{\sum a_i \sigma_i}\!\alpha = \sum a_i \int_{\sigma_i}\!\alpha = \sum a_i\int_{\Delta^p}\!\sigma_i^*\alpha.\]
以下、例題 1.6.9 で見たストークスの定理の単体バージョンを考えたい。
写像 \(\fn{\eps_k}{\Delta^{p - 1}}\Delta^p\) を次で定義する:
\[\begin{split}\eps_k\colon (x_1, \dotsc, x_{p - 1}) \longmapsto \begin{cases} (1, x_1, \dotsc, x_{p - 1}) & \quad \text{if } k = 0\\ (x_1, \dotsc, x_k, x_k, \dotsc, x_{p - 1}) & \quad \text{if } 0 < k < p\\ (x_1, \dotsc, x_{p - 1}, 0) & \quad \text{if } k = p \end{cases}\end{split}\]試しに二次元から三次元の \(\eps_k\) を書き出してみる。三角形から四面体各面への四つの写像を意味する:
\[\begin{split}\begin{align*} \eps_0(x_1, x_2) &= (1, x_1, x_2)\\ \eps_1(x_1, x_2) &= (x_1, x_1, x_2)\\ \eps_2(x_1, x_2) &= (x_1, x_2, x_2)\\ \eps_3(x_1, x_2) &= (x_1, x_2, 0) \end{align*}\end{split}\]\(\eps_0, \eps_p\) は幾何的には合同変換。埋め込みのようなものか。
それ以外でも微分同相写像のように思える。
境界 \(\partial \sigma\) を次で定義する:
\[\partial \sigma = \sum_{k = 0}^p (-1)^k \sigma \circ \eps_k.\]
定理 3.2.1: ストークスの定理単体バージョン
\(\sigma\) を特異 \(p\) 単体、\({\alpha \in \varOmega^{p - 1}(M)}\) とすると:
\[\int_\sigma\!\dd\alpha = \int_{\partial \sigma}\!\alpha.\]証明の方針は、まず \(\sigma^*\alpha\) を次のように表したときに:
\[\begin{split}\begin{align*} \sigma^*\alpha &= \sum_{k = 1}^{p - 1}\alpha_k = \sum_{k = 1}^{p - 1}(-1)^k f_k \dd x_1 \wedge \dotsb \wedge \dd x_{k - 1} \wedge \dd x_{k + 1} \dotsb \wedge \dd x_p, \\ \sigma^* \dd\alpha &= \dd \sigma^*\alpha = \sum_{k = 1}^p \frac{\partial f_k}{\partial x_k}\dd x_1 \wedge \dd x_p \end{align*}\end{split}\]和の各項における、次の等式を示されれば、主張も示されることになる:
\[\int_{\Delta^p}\!\frac{\partial f_k}{\partial x_k}\dd x_1 \wedge \dotsb \wedge \dd x_p = \int_{\sum_{i = 0}^p(-1)^i\eps_i}\!\alpha_k.\]以下、\({k = p}\) のときとそれ以外とで場合分けして示す。
\({k = p}\) のとき:
\[\begin{split}\begin{align*} \int_{\Delta^p}\!\frac{\partial f_p}{\partial x_p}\,\dd x_1 \wedge \dotsb \wedge \dd x_p &= \int_{x_1 = 0}^1\dotsi\int_{x_p = 0}^{x_{p - 1}}\!\frac{\partial f_p}{\partial x_p}\,\dd x_p \dots \dd x_1\\ &= \int_{x_1 = 0}^1\dotsi\int_{x_{p - 1} = 0}^{x_{p - 2}}\!f_p(x_1, \dotsc, x_{p - 1}, x_{p - 1}) - f_p(x_1, \dotsc, x_{p - 1}, 0)\,\dd x_{p - 1} \dots \dd x_1\\ &= \int_{\eps_{p - 1} - \eps_p}\!(-1)^{p - 1}\alpha_p\\ &= \int_{(-1)^{p - 1}\eps_{p - 1} + (-1)^p\eps_p}\!\alpha_p\\ &= \int_{\sum_{i = 0}^p (-1)^i\eps_i}\!\alpha_p. \end{align*}\end{split}\]最初の等号は単体に沿う積分の定義そのもの。
二番目の等号は中央の定積分を展開しただけ。
三番目の等号。ここがわからない。かなりギャップがあるような。
四番目の等号は \({i \ne p - 1, p}\) ならば \(\displaystyle {\int_{\eps_i}\!(-1)^p\alpha_p = 0}\) から導かれる。
最後の等号は和をシグマ記号にまとめただけ。
となって OK となる。
\({k \lt p}\) のとき:細かい技巧があるようだ。
\(\displaystyle {F(x_1, \dotsc, x_k)} = {\int_{x_{k + 2} = 0}^{x_{k + 1}}\dotsi\int_{x_p = 0}^{x_{p - 1}}\!\frac{\partial f_k}{\partial x_k}\,\dd x_p \dots \dd x_{k + 2}}\) とおく。
ふつうのニ変数の積分の順序交換により、次のように書き換えられる:
\[\int_{x_k = 0}^{x_{k - 1}}\int_{x_{k + 1} = 0}^{x_k}\!F(\cdot)\,\dd x_{k + 1}\dd x_k = \int_{x_{k + 1} = 0}^{x_{k - 1}}\int_{x_k = x_{k + 1}}^{x_{k - 1}}\!F(\cdot)\,\dd x_k\dd x_{k + 1}.\]この右辺の内側の定積分を展開すると次のようになる:
\[\int_{x_{k + 2} = 0}^{x_{k + 1}}\dotsi\int_{x_p = 0}^{x_{p - 1}}\! f_k(x_1, \dotsc, x_{k - 1}, x_{k - 1}, x_{k + 1}, \dotsc, x_p) - f_k(x_1, \dotsc, x_{k - 1}, x_{k + 1}, x_{k + 1}, \dotsc, x_p)\, \dd x_p \dots \dd x_{k + 2}.\]
以上を利用して:
\[\begin{split}\begin{align*} \int_{\Delta^p}\!\frac{\partial f_k}{\partial x_k}\,\dd x_1 \wedge \dotsb \wedge \dd x_p &= \int_{x_1 = 0}^1\dotsi\int_{x_{k - 1} = 0}^{x_{k - 2}}\int_{x_{k + 1} = 0}^{x_{k - 1}}\int_{x_{k + 2} = 0}^{x_{k + 1}}\dotsi\int_0^{x_{p - 1}} \!f_k(\cdot) - f_k(\cdot)\, \dd x_p \dots \dd x_{k + 2} \dd x_{k + 1} \dd x_{k - 1} \dots \dd x_1\\ &= \int_{\eps_{k - 1} - \eps_k}\!(-1)^{k - 1}\alpha_k\\ &= \int_{(-1)^{k - 1}\eps_{k - 1} + (-1)^k\eps_k}\!\alpha_k\\ &= \int_{\sum_{i = 0}^k (-1)^i\eps_i}\!\alpha_k. \end{align*}\end{split}\]最初の等号:単体に沿う積分の定義に上記を加味した変形による。
二番目の等号:\({k + 1}\) 以降を \(k\) に置き換えることで得られるらしい。
三番目の等号:\({j \ne k - 1, k}\) ならば \(\displaystyle {\int_{\eps_i}\!(-1)^k\alpha_k = 0}\) から導かれる。
以降の等号成立の理由については先ほどの場合を参照。
となって OK となる。
以上でストークスの定理単体バージョンが示された。
上記定理の検討?
特異 \(p\) チェインの次の集合を定義する:
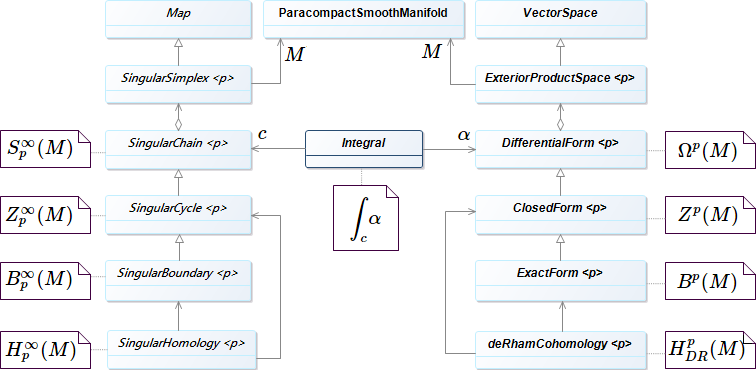
\[S_p^\infty(M) = \Set{\sum_i^{\text{finite}}a_i \sigma_i \Sth a_i \in \RR,\ \sigma_i \in C^\infty(\Delta^p, M)}\]このとき、次の双線型写像が考えられる(ストークスの定理が成り立つ):
\[S_p^\infty(M) \times \varOmega^p(M) \longto \RR, \quad (c, \alpha) \longmapsto \int_c\!\alpha = \sum a_i \int_{\sigma_i}\!\alpha\]境界準同型 \(\partial\) が特異 \(p\) チェイン全体 \(S_*^\infty(M)\) に対して定義されていて \({\partial \circ \partial = 0}.\) そこで次の系列は複体となり、これを \(C^\infty\) 級特異単体複体という:
\[\require{amscd} \begin{CD} 0 @<{\partial}<< S_0^\infty(M) @<{\partial}<< S_1^\infty(M) @<{\partial}<< \cdots \end{CD}\]\({Z_p^\infty(M) = \ker(\fn{\partial}{S_p^\infty}S_{p - 1}^\infty)}\) の元を \(p\) 次元 \(C^\infty\) 級特異サイクルという。
\({B_p^\infty(M) = \im(\fn{\partial}{S_{p + 1}^\infty}S_p^\infty)}\) の元を \(p\) 次元 \(C^\infty\) 級特異バウンダリーという。
\({H_p^\infty(M) = Z_p^\infty(M) / B_p^\infty(M)}\) を \(p\) 次元 \(C^\infty\) 級特異ホモロジー群という。
\({\alpha \in Z^p(M)}\) と \({\beta \in B^{p - 1}(M)}\) とが \({\alpha = \dd \beta}\) を満たすならば、積分 \(\displaystyle {\int_c\!\alpha} = {\int_c\!\dd \beta} = {\int_{\partial c}\!\beta}\) は \({\partial c = 0}\) なる \(c\) に対しては常にゼロである。
\({\alpha \in Z^p(M)}\) と \({c \in S_p^\infty(M)}\) について \({\int_c\!\alpha = 0} \implies {\exists \beta \in B^{p - 1}(M)}\text{ s.t. }{\alpha = \dd \beta}.\)
\({c \in S_p^\infty(M)} \iff {\partial c = 0}.\)
\({c \in B_p(M)}\) であって \({c = \partial b}\) であるとするならば、 \({\forall \alpha \in Z^p(M)},\ \displaystyle {\int_c\!\alpha} = {\int_{\partial b}\!\alpha} = {\int_b\!\dd \alpha} = 0.\)
\(H_p^\infty(M)\) の基底の各代表 \({c_i \in S_p^\infty(M)}\) に対して \(\displaystyle {\int_{c_i}\!\alpha = 0} \implies {\alpha = \dd \beta}.\)
\({k = \dim H_p^\infty(M) = \dim \H^p(M)}\) とし、基底 \([c_1], \dotsc, [c_k] \in H_p^\infty(M)\) と \({\alpha \in Z^p(M)}\) が \(\displaystyle {\int_{c_i}\!\alpha = 0}\) を満たすならば \({\exists \beta \in B^{p - 1}(M)}\text{ s.t. }{\alpha = \dd \beta}.\)
cf. 例題 3.3.1
注意 3.2.2: \(C^\infty\) 級特異単体複体のチェインを定義する係数を整数にするとどうなるかを説明している。
問題 3.2.3: ホモトピックサイクルについては積分が一致する
\({c_0, c_1 \in S_p^\infty(M)}\) がホモトピックサイクルであるとは、 \(\displaystyle {c_t = \sum_i a_i \sigma_i^{(t)}}\quad{(t \in [0, 1])}\) が写像 \({(t, x) \longmapsto \sigma_i^{(t)}(x)}\) が滑らかであるように与えられていることをいう。
\({\alpha \in Z^p(M)}\) に対して \(\displaystyle {\int_{c_0}\!\alpha = \int_{c_1}\!\alpha}.\)
写像 \(\fn{F_i}{[0, 1]\times \Delta^p}{M}{(x, t)}\sigma_i^{(t)}(x)\) を定義する。
\[\partial F_i = \sigma_0^{(1)} - \sigma_0^{(0)} - \sum_{k = 0}^p (-1)^k F_i \circ (\id, \eps_k).\]\({c_i \in S_p^\infty(M)}\) の性質によって:
\[\begin{split}\begin{align*} &\partial c_t = \sum_i a_i \sum_{k = 0}^p \sigma_i^{(t)}\circ \eps_k = 0,\\ &\text{i.e. } \sum_i a_i \sum_{k = 0}^p (-1)^k F_i \circ (\id, \eps_k) = 0.\\ &\therefore \partial \sum_i a_i F_i = \sum_i a_i \sigma_i^{(1)} - \sum_i a_i \sigma_i^{(0)} = c_1 - c_0. \end{align*}\end{split}\]定理 3.2.1 および 例題 1.6.9 のどちらかを利用できる。ストークスの定理を \({[0, 1] \times \Delta^p}\) からの写像に沿って考えるか、\({[0, 1] \times \Delta^p}\) を単体に分割して考えることで次を得る:
\[\begin{split}\begin{align*} 0 = \int_F\!\dd\alpha &= \int_{\partial F}\!\alpha\\ &= \int_{c_1}\!\alpha - \int_{c_0}\!\alpha. \end{align*}\end{split}\]