第 3 章 微分形式の積分 2/3¶
3.3 単体的ドラーム理論(展開)¶
目標は次のとおり:
\(\varOmega^*(M)\) の \(p\) 次元コホモロジー群と単体複体のコホモロジー群は一致する。
単体複体のコホモロジー群とホモロジー群は同次元の双対空間である。
これらが言えれば \({\H^p(M) \cong \RR^d}\) のときに次の条件を満たす \(c_1, \dotsc, c_d \in Z_p^\infty(M)\) が存在することになる:
3.3.1 単体複体¶
有限単体複体を定義するために、記号と用語をいくつか導入する。
読者ノート
本書では頂点の記号に \(e_i\) を用いているが、これをユークリッド空間の基底である必要がある勝手に勘違いしてしまったので、本ノート中は別の記号を割り当てる。
\(k\) 次元単体 \(\langle v_{i_0} \dots v_{i_k}\rangle\)
\(k\) 次元単体とは \(\RR^k\) 内の \({k + 1}\) 個の頂点で構成される凸包であり、各点は一般の位置にあるものとする。
「各点が一般の位置にある」とは、例えば次のベクトルが一次独立であることを意味する:
\[v_1 - v_0, v_2 - v_0, \dotsc, v_{k + 1} - v_0.\]
重心座標 \({(t_{i_0}, \dotsc, t_{i_k})}\)
\(k\) 次元単体の点を \(\displaystyle {\sum_{l = 0}^k t_{i_l} v_{i_l}}\) で表したときの基底に対する係数を組にした \({(t_0, \dotsc, t_k)}\) を重心座標と呼ぶ。
各座標成分が非負であることと、座標成分の和が 1 であることに注意。
\(k\) 次元単体の内部とは、重心座標のどの成分も正となるような点のなす部分と解釈する。特に境界は内部に含まれない。
定義 3.3.1: 有限単体複体
単数または複数の \(k\) 次元単体からなる有限集合で、さらに次の条件を満たすものを有限単体複体という:
境界を構成するすべての \({k - 1}\) 単体も \(K\) に含まれる。
\[\langle v_{i_0} \dots v_{i_k}\rangle \in K \implies \langle v_{i_0} \dots v_{i_{l - 1}} v_{i_{l + 1}} \dots v_{i_k}\rangle \in K.\]この規則が再帰的に適用されるので、自動的に全頂点までも \(K\) に含まれることになる。
\(K\) のどの二つの単体についても、それらの共通部分が \(K\) に含まれる。
\(\displaystyle {\abs{K} = \bigcup_{\sigma \in K}\sigma}\) を 幾何的実現 という。
ユークリッド空間の部分集合、点の集まりとして素朴に解釈すればよい。
したがって元は重心座標で表される。
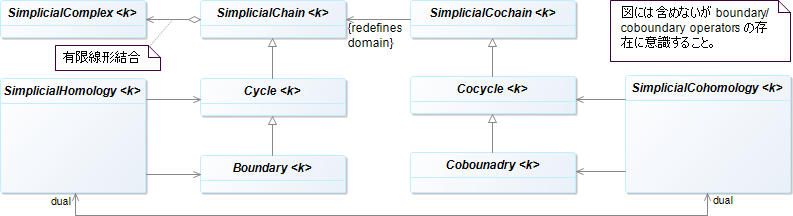
\(k\) チェイン
\(k\) チェインとは有限単体複体 \(K\) を決めたときの、その \(k\) 単体の実係数有限線形結合である。記号 \(C_k(K)\) で表す。
\(C_k(K)\) は \(k\) 単体の個数と同じ次元のベクトル空間である。その個数を \(n\) とすると、次のように書ける:
\[C_k(K) = \Set{\sum_{i = 1}^n a_i \sigma_i \Sth a_i \in \RR, \sigma_i \in K}.\]
境界、境界準同型
単体 \({\sigma \in K}\) の境界 \({\partial \sigma}\) を次で定義する:
\[\partial \sigma = \sum_{j = 0}^k(-1)^j \langle v_{i_0} \dots v{i_{j - 1}} v_{i_{j + 1}} \dots v_{i_k}\rangle.\]0 単体(頂点、点)の境界はゼロ、
1 単体(辺、線分)の境界は 0 単体(頂点、点)、
2 単体(面)の境界は 1 単体(辺、線分)、
……となる。というわけで
境界準同型 or 境界演算子 \(\fn{\partial}{C_k(K)}C_{k - 1}(K)\) が定義される。
\({\partial \circ \partial = 0}\) という性質がある。
このゼロ準同型の性質より、複体 \(C_*(K)\) が得られる:
\[\require{amscd} \begin{CD} 0 @<{\partial}<< C_0(K) @<{\partial}<< C_1(K) @<{\partial}<< C_2(K) @<{\partial}<< \cdots \end{CD}\]さらに実係数ホモロジー群が得られる:
\[H_k(K) = \ker(\fn{\partial}{C_k(K)}C_{k - 1}(K)) /{\im(\fn{\partial}{C_{k + 1}(K)}{C_k(K)})}\]例によって \({Z_k(K) = \ker(\fn{\partial}{C_k(K)}C_{k - 1}(K))}\) をサイクル、\(\im(\fn{\partial}{C_{k + 1}(K)}{C_k(K)})\) をバウンダリーと呼ぶ。
実係数であることは、チェインを実係数で構成したことから来ている。
\(k\) コチェイン
\(K\) の \(k\) 単体のなす有限集合上の実数値関数を \(k\) コチェインという。
\(k\) コチェインからなる有限次元ベクトル空間を \(C^k(K)\) と書く。
\(C^k(K)\) は \(C_k(K)\) の双対ベクトル空間である。
\(\fn{\delta}{C^k(K)}C^{k + 1}(K)\) を次で定義する:
\[(\delta c)(i_0, \dotsc, i_{k + 1}) = \sum_{l = 0}^{k + 1}(-1)^l c(i_0, \dotsc, i_{l - 1}, i_{l + 1}, \dotsc, i_{k + 1})\]\({(\delta c)(\sigma) = c(\delta \sigma)}.\)
\({\delta \circ \delta = 0}\) が成り立つ。これは \({\partial \circ \partial = 0}\) による。
\(K\) のコホモロジー群は \(K\) のコチェイン複体 \(C^*(K)\) のコホモロジー群として定義される:
\[\begin{CD} 0 @>{\delta}>> C^0(K) @>{\delta}>> C^1(K) @>{\delta}>> C^2(K) @>{\delta}>> \cdots \end{CD}\]\[H^k(K) = \ker(\fn{\delta}{C^k(K)}C^{k + 1}(K)) / \im(\fn{\delta}{C^{k - 1}(K)}C^k(K))\]
定義 3.3.2: オイラー標数
\({\dim C_k(K) = \dim C^k(K)}\) は \(k\) 単体の個数 \(m_k\) である。
\(K\) の単体の次元が高々 \(n\) であるとき次の値を \(K\) のオイラー(・ポアンカレ)標数という:
\[\chi(K) = \sum_{k = 0}^n(-1)^k m_k.\]
問題 3.3.3: \(\displaystyle {\chi(K) = \sum_{k = 0}^n(-1)^k \dim H_k(K)} = {\sum_{k = 0}^n(-1)^k \dim H^k(K)}\)
複体 \(C_*(K)\) においては
\({\dim H_k(K) = \dim\ker \partial_k - \dim\im \partial_{k + 1}}\) と
準同型定理 \({\dim\im\partial_{k + 1} = \dim C^{k + 1} - \dim\ker \partial_{k + 1}}\)
を利用する。複体 \(C^*(K)\) においても、上の二つに対応する性質を利用する。
命題 3.3.4: \({\dim H_k(K) = \dim H^k(K)}\)
こちらの証明は線形代数。内積を利用するようだ。
\(C_*(K)\) の基底を何かとって \(C_k(K)\) が列ベクトル表示されるものとする。
境界準同型 \(\partial\) を行列 \(A, B\) を用いて表すものとする。このとき \({\partial \circ \partial = 0}\) から \({AB = O}\) を満たす。
\[\begin{CD} C_{k - 1}(K) @<{\partial}<{A}< C_k(K) @<{\partial}<{B}< C_{k + 1}(K) \end{CD}\]同時に \(C^*(K)\) は行ベクトル表示されるものとする。これはコチェインが \(C_k(K)\) 上の微分形式であることによる。準同型 \(\delta\) は行ベクトルに作用するとみなせば同じ \(A, B\) で表される:
\[\begin{CD} C^{k - 1}(K) @>{\delta}>{A}> C^k(K) @>{\delta}>{B}> C^{k + 1}(K) \end{CD}\]\(C^k(K)\) と \(C_k(K)\) の間の「積」をユークリッド空間の内積として定義する。
直交補空間の性質をこの証明で利用したい。
行列 \(A\) を行ベクトル \(\bm a_i\ {(i = 1, \dotsc, l)}\) を縦に並べたものとすると、\(\ker\partial = \operatorname{span}{({}^t\!\bm a_1, \dotsc, {}^t\!\bm a_l)}^\perp.\)
行列 \(B\) を列ベクトル \(\bm b_i\ {(i = 1, \dotsc, n)}\) を横に並べたものとすると、\(\im\partial = \operatorname{span}{(\bm b_1, \dotsc, \bm b_n)}.\)
\({\im\partial \subset \ker\delta}\)
以上より次が成り立つ:
\[\operatorname{span}(\bm b_1, \dotsc, \bm b_n) \subset \operatorname{span}({}^t\!\bm a_1, \dotsc, {}^t\!\bm a_l)^\perp.\]
一方、
\({\ker\delta = \operatorname{span}(\bm b_1, \dotsc, \bm b_n)^\perp,}\)
\({\im\delta = \operatorname{span}({}^t\!\bm a_1, \dotsc, {}^t\!\bm a_l),}\)
\({\im\delta \subset \ker\delta}\)
以上より次が成り立つ:
\[\operatorname{span}({}^t\!\bm a_1, \dotsc, {}^t\!\bm a_l) \subset \operatorname{span}(\bm b_1, \dotsc, \bm b_n)^\perp.\]ここで
\[V = \operatorname{span}({}^t\!\bm a_1, \dotsc, {}^t\!\bm a_l)^\perp \cap \operatorname{span}(\bm b_1, \dotsc, \bm b_n)^\perp\]とおくと、
\[\operatorname{span}({}^t\!\bm a_1, \dotsc, {}^t\!\bm a_l)^\perp /\operatorname{span}(\bm b_1, \dotsc, \bm b_n) \cong V \cong \operatorname{span}(\bm b_1, \dotsc, \bm b_n)^\perp /\operatorname{span}({}^t\!\bm a_1, \dotsc, {}^t\!\bm a_l).\]すなわち \({\ker\delta/\im\delta} \cong V \cong {\ker\delta/\im\delta}\) が成り立つ。したがって \({\dim H_k(K) = \dim H^k(K)}\) である。
注意 3.3.5: \(C^k(K)\) と \(C_k(K)\) との間の積は \(H^k(K)\) と \(H_k(K)\) との間の積を引き起こす。
3.3.2 単体複体上の微分形式¶
定義 3.3.6: \({\varOmega^k(K)},\ {\H^*(K)}\)
\({\omega \in \varOmega^k(K)}\) を次の二点で定義する:
\(K\) のすべての単体から、その上の \(k\) 形式への対応である: \({\sigma \longmapsto \omega_\sigma}.\)
\(m\) 単体 \(\sigma\) とその面である \(m - 1\) 単体 \(\tau\) に対して \({\omega_\sigma|\tau = \omega_\tau}\) となる。
外微分 \(\fn{\dd{}}{\varOmega^k(K)}\varOmega^{k+1}(K)\) について
\({\dd{} \circ \dd{} = 0}\)
\({\H^*(K) = \ker{\dd{}}/\im{\dd{}}}\)
が定義される。
2.10 節の理論を \(K\) のドラーム複体 \(\varOmega^*(K)\) に適用することができる。その結果 \({\H^*(K) \cong H^*(K)}\) と結論できる。
開星状体 \(O(v_i)\) の定義中にある「単体の内部の和集合」がわからない。これは \({v_i \notin O(v_i)}\) を意味する?
3.3.3 単体的ドラームの定理¶
単体上の積分が \(K\) の \(\varOmega^*(K)\) と \(C^*(K)\) の関係を与える。
\(\Delta^k\) から \(\sigma = {\langle e_{i_0} \dots e_{i_k}\rangle}\) への写像をやはり同じ記号で記す:
\[\sigma(x_1, \dotsc, x_k) = (1 - x_1)e_{i_0} + (x_1 - x_2)e_{i_1} + \dotsb + (x_{k - 1} - x_k)e_{i_{k - 1}} + x_k e_{i_k}.\]写像 \(\fnm{I}{\varOmega^*(K)}{C^*(K)}{(\omega, \sigma)}\int_\sigma\!\omega \in \RR\) は \(K\) の \(k\) コチェインを与える。
\(I\) は 定理 3.2.1 により、\({I \circ \dd{}} = {\delta \circ I}\) が成り立つコチェイン写像である。
定理 3.3.7: 単体ドラームの定理
\(I\) は \(\H^*(K)\) と \(H^*(K)\) の間の同型写像を誘導する。
コチェイン写像 \(\fn{s}{C^*(K)}\varOmega^*(K)\) で \({I \circ s} = \id_{C^*(K)}\) を満たすものを考える。
次の事実を利用する:
\(\fn{I}{\varOmega^*(K)}C^*(K)\) は値 \(\displaystyle {\int_\sigma\!\omega}\) を対応させる写像であり、\({I \circ \dd{}} = {\delta \circ I}\) である。
\(I\) は準同型写像 \(\fn{I_*}{\H^*(?)}H^*(K)\) を誘導する。さらに \({\H^*(?) \cong H^*(K)}\) および次元が有限であることから同型写像である。
\(s\) は準同型写像 \(\fn{s_*}{H^*(K)}\H^*(?)\) を誘導し、 \({I_* \circ s_* = \id_{H^*(K)}}\) を満たす。
\({c \in C^0(K)}\) に対し \(\varOmega^0(K)\) の何が対応するのか、どのような \(\abs{K}\) 上の関数であればよいのかを考える。それは頂点 \(e_i\) で値 \(c(i)\) をとる関数を線形に拡張するのがよい:
\(\sigma = {{\langle e_{j_0} \dots e_{j_m}\rangle} \in K}\) 上で \(\displaystyle s(c)_{\sigma} = \sum_{l = 0}^m c(j_l)t_{j_l}\) である。
\(\dd{s(c)_\sigma}\) の計算をする:
\[\begin{split}\begin{align*} \dd{s(c)_\sigma} &= \sum_{l = 0}^m c(j_l) \dd{t_{j_l}}\\ &= \sum_{\set{i_0, i_1} \subset \set{j_0, \dotsc, j_m}} (c(i_0) - c(i_1)) \omega_{i_0 i_1}. \end{align*}\end{split}\]上の式変形には p. 107 の式やシグマの展開を行なう。
ここで \({i_0 \lt i_1}\) としておく。上の式が \(\delta c\) の像であるには \(\delta {c(i_0, i_1)} = {c(i_0) - c(i_1)}\) であることから \({c^1 \in C^1(K)}\) に対して次のように定義できることが必要である:
\[s(c^1)_\sigma = \sum_{\set{i_0, i_1} \subset \set{j_0, \dotsc, j_m}} c^1(i_0, i_1) \omega_{i_0 i_1}.\]一般の \({c \in C^k(K)}\) に対しては次のように \(s\) を定義する:
\[s(c)_\sigma = \sum_{\set{i_0, \dotsc, i_k} \subset \set{j_0, \dotsc, j_m}} c(i_0, \dotsc, i_k) \omega_{i_0 \dots i_k} \quad (m \ge k,\ \sigma = \langle e_{j_0} \dots e_{j_m}\rangle).\]\({\dd{}\circ s = s \circ \delta}\) を示す。そのために \({\dd{s(c)_\sigma} = s(\delta(c))_\sigma}\) を示す。
最初の等号は上記 \(s(c)_\sigma\) の定義に外微分を分配することによる。
二番目の等号は標準 \(k\) 形式の外微分の定義 (p. 108) による。
三番目の等号はシグマの展開か。
四番目の等号は \(\delta\) の定義 (p. 102) を当てはめる。
最後の等号は上記 \(s(c)_\sigma\) の定義で \(c\) を \(\delta c\) に置き換えると得られる。
\({s(c)\ (c \in C^k(K))}\) を \(\sigma = {\langle e_{i_0} \dots e_{i_k}\rangle}\) 上で積分するには、\(\sigma\) を含む任意の単体 \({\langle e_{j_0} \dots e_{j_m}\rangle}\) で次のようにする:
\[\begin{split}\begin{align*} (I \circ s)(c)(i_0, \dotsc, i_k) &= \int\sigma\! \sum_{\set{l_0, \dotsc, l_k} \subset \set{j_0, \dotsc, j_m}} c(l_0, \dotsc, l_k) \omega_{l_0, \dotsc, l_k}\\ &= \sum_{\set{l_0, \dotsc, l_k} \subset \set{j_0, \dotsc, j_m}} c(l_0, \dotsc, l_k) \int\sigma\! \omega_{l_0, \dotsc, l_k}\\ &= c(i_0, \dotsc, i_k). \end{align*}\end{split}\]
3.3.4 多様体の三角形分割と単体的ドラーム理論¶
同相写像 \(\fn{\varphi}{\abs{K}}M\) が各単体上で \(C^\infty\) 級となるものを \(M\) の \(C^\infty\) 級 三角形分割 という。
次の三点により \(\varphi^*\) が \(\H^*(M)\) と \(\H^*(K)\) の同型を与えている:
\({\H^*(M) \cong H^*(K)}.\)
\({\H^*(K) \cong H^*(K)},\) 3.3.2 節参照。
\(\fn{\varphi^*}{\varOmega^*(M)}\varOmega^*(K)\) の存在。
\(\varOmega^*(K)\) と \(C^*(K)\) のコホモロジー群の同型も単体に沿う積分から誘導される。
\(H_p(K)\) の生成元 \([c_1], \dotsc, [c_k]\) に対し、 \(\displaystyle {\int_{c_i}\!\alpha = 0}\) となる \({\alpha \in Z^p(M)}`は :math:`{\alpha \in B^p(M)}\) を満たす。
三角形分割のとり方に依らないので \(\varOmega^*\) と \(C^*\) が等しい?
オイラー標数は多様体に対して定まる量になっている。
3.4 向きを持つ多様体上の積分¶
直方体あるいは単体からの写像には自然に向きが定まっている。
コンパクト \(n\) 次元多様体は \(n\) 次元単体からの \(C^1\) 級の写像の像でうまく覆うことができる。
多様体に向きが定まっているときは、積分をすることができる。
定義 3.4.1: 向き付けを持つ or 向き付け可能である多様体
幾何学 I 3.6 節 参照。
定義 3.4.2: 向き付けられている多様体
ユークリッド空間には、その座標の順による向きが定まっている。例えば直方体の積分の定義にそれが表れている。
向き付けを持つことと、向き付けられていることは別の概念であるらしい。上記のリンク先も参照。
定義 3.4.3: 微分形式の台
関数の台と定義は似ているが、\(\alpha(x)\) という式が気になる。
\({\alpha \in \varOmega^n(M)}\) ということは \({\alpha = f(\bm x)}\,{{\dd x_1} \wedge \dotsb \wedge {\dd x_n}}\) となる多様体上の関数 \(f\) が局所的に存在するということだ。この局所座標近傍を \({(U, \varphi)}\) とし、コンパクト集合 \({K \subset U}\) をとる。このときコンパクト集合 \(\varphi(K)\) を有限個の disjoint な直方体で被覆できる。この直方体の逆像を \(\kappa\) とすると、次の式で積分をうまく定義できる:
これを \(\alpha\) の \(\varphi\inv\) に沿う積分と呼ぶ。
定義 3.4.4: \(U\) のコンパクト部分 \(K\) に台を持つ \(\alpha\) の \(\varphi\inv\) に沿う積分
\[\int_{\varphi\inv}\!\alpha = \int_{\varphi(U)}\!f(\bm x)\,\dd x_1 \dots \dd x_n.\]
以下、多様体は向き付けられているものとする。
命題 3.4.5: 座標近傍の取り方に依らない
座標近傍 \(U, V\) の共通部分のコンパクト部分集合 \(K\) に台を持つ \(\alpha\) の積分の値は等しい:
\[\int_{\varphi\inv}\!\alpha = \int_{\psi\inv}\!\alpha.\]\({(V, \psi)}\) から見て \({\alpha = g(\bm y)}\,{{\dd y_1} \wedge \dotsb \wedge {\dd y_n}}\) と表す。
座標変換 \({\varphi \circ \psi\inv}\) を考える: \({(\varphi \circ \psi\inv)(\bm y)} = {(x_1(\bm y), \dotsc, x_n(\bm y))}\)
\[\begin{split}\begin{align*} g(\bm y)\,\dd y_1 \wedge \dotsb \wedge \dd y_n &= f(x_1(\bm y), \dotsc, x_n(\bm y))\,\dd x_1 \wedge \dotsb \wedge \dd x_n\\ &= f(x_1(\bm y), \dotsc, x_n(\bm y)) \det\frac{\partial(x_1, \dotsc, x_n)}{\partial(y_1, \dotsc, y_n)}\,\dd y_1 \wedge \dotsb \wedge \dd y_n. \end{align*}\end{split}\]ここまではよく見かける論証。
積分は次のようになる:
\[\begin{split}\begin{align*} \int_{\varphi\inv|\varphi(U \cap V)}\!\alpha &= \int_{\varphi(U \cap V)}\!f(\bm x)\,\dd x_1 \dots \dd x_n\\ &= \int_{\psi(U \cap V)}\! f(x_1(\bm y), \dotsc, x_n(\bm y)) \Abs{\det{\frac{\partial(x_1, \dotsc, x_n)}{\partial(y_1, \dotsc, y_n)}}}\,\dd y_1 \dots \dd y_n\\ &= \int_{\psi(U \cap V)}\! g(\bm y)\,\dd y_1 \dots \dd y_n\\ &= \int_{\psi\inv|\psi(U \cap V)}\!\alpha. \end{align*}\end{split}\]最初と最後の等号は 定義 3.4.4 による。
二番目の等号は重積分の変数変換か?
三番目の等号は多様体が向き付けられていることにより、絶対値を取らなくても行列式の符号が正であることによる。
命題 3.4.6: 向き付けられた二つの座標近傍系にそれぞれに従属する 1 の分割についての等式
\[\sum_i \int_{\varphi\inv}\!\lambda_i\alpha = \sum_j \int_{\psi\inv}\!\mu_j\alpha.\]証明は、開被覆 \(\set{U_i \cap V_j}\) およびそれに従属する 1 の分割 \(\set{\lambda_i \mu_j}\) を考えて 命題 3.4.5 を用いる。
定義 3.4.7: コンパクトで向き付けられた多様体上の微分形式の積分
\[\int_M\!\alpha = \sum_i \int_{\varphi\inv}\!\lambda_i \alpha.\]\(\set{(U_i, \varphi_i)}\) に従属する 1 の分割を用いている。
この定義が well-defined であることは、命題 3.4.6 による。
定理 3.4.8: ドラーム・コホモロジー群の性質
コンパクト・向き付けを持つ・連結 \(n\) 次元多様体 \(M\) について \({\H^n(M) \cong \RR.}\)
写像 \(\displaystyle {{\varOmega^n(M) \owns \alpha} \longmapsto {\int_M\!\alpha} \in \RR}\) は同型写像 \({\H^n(M) \longto \RR}\) を誘導する。
これがまともな準同型であることをまず示す。
\(\alpha\) が向き付けを持つ \({(U, (x_1, \dotsc, x_n))}\) 上に台を持ち、非負関数を用いて \({\alpha = f}\,{{\dd x_1} \wedge \dotsb \wedge {\dd x_n}}\) の形に書けるとする。
このときに \(\displaystyle {\int_M\!\alpha \gt 0}\) となるから、ゼロ準同型ではない。
あとは \({\H^n(M) \le 1}\) を示す。
例題 3.4.9: モース関数を利用した 定理 3.4.8 の証明
2.8 節 で多用した技法を採用する。
\({\varnothing = N_0 \subset N_1 \subset \dotsb \subset N_k = M}\)
\({j \lt k}\) のとき \({N_{j - 1}\cap B_j}\) は
空集合であるか、
\({B^{n - m_j} \times S^{m_j}}\) と微分同相であり、
\({N_{k - 1} \cap B_k}\) は \({B^1 \times S^{n - 1}}\) と微分同相である。
定理 2.8.1 のマイヤー・ビエトリス完全系列を見ると、 \({j \lt k}\) のとき \({\dim\H^n(N_j) = 0.}\)
よって \({\dim\H^n(M) \le 1.}\)
至るところゼロでない微分形式が存在するならば、多様体は向き付け可能である。
命題 3.4.10: \(M\) が境界なし・向き付け不可能・コンパクト・連結ならば \({\H^n(M) \cong H_n(K) \cong 0}\)
\(M\) は向き付け不可能であるが、幾何学 I 3.6 節 にあるように次のような多様体 \(\widehat M\) と写像 \(\varphi\) がとれる:
\(\widehat M\) は向き付け可能・連結であり、
写像 \(\fn{\varphi}{\widehat M}\widehat M\) は向きを反対にし、不動点がない。
\({\varphi \circ \varphi = \id_{\widehat M},}\)
\({{\widehat M/\varphi} \cong M.}\)
ここで \({\alpha \in \varOmega^n(M)}\) をとり、射影を \(\fn{\pi}{\widehat M}M\) とおく。
\({\pi = \pi \circ \varphi}\) ゆえ \({\varphi^*\pi^*\alpha = \pi^*\alpha.}\) したがって:
\[\int_{\widehat M}\!\varphi^*\pi^*\alpha = \int_{\widehat M}\!\pi^*\alpha.\]写像 \(\varphi\) の反変性により:
\[\int_{\widehat M}\!\varphi^*\pi^*\alpha = -\int_{\widehat M}\!\pi^*\alpha.\]この二つの等式より:
\[\int_{\widehat M}\!\pi^*\alpha = 0.\]ここで 定理 3.4.8 により、\({{\pi^*\alpha} = {\dd \beta} \in \varOmega^n(M)}\) (外微分をオメガの元と見るのが新鮮)
\(\displaystyle {\beta_1 = \frac{1}{2}(\beta + \varphi^*\beta) \in \varOmega^{n - 1}(\widehat M)}\) に対して、\({\varphi^*\beta_1 = \beta_1}\) より \({\beta_1 = \pi^*\beta_2 \in \varOmega^{n - 1}(\widehat M).}\)
\[\begin{split}\begin{align*} \pi^*(\dd \beta_2) &= \dd(\pi^*\beta_2) = \dd \beta_1\\ &= \frac{1}{2}\dd(\beta + \varphi^*\beta)\\ &= \frac{1}{2}(\dd \beta + \varphi^* \dd \beta)\\ &= \frac{1}{2}(\pi^*\alpha + \varphi^*\pi^*\alpha)\\ &= \pi^*\alpha. \end{align*}\end{split}\]\(\pi\) が単射だからか \({\dd \beta_2 = \alpha}\) となる。