94 日目(曇り)傘は要らなかった
0:20 昭和レトログッズの映像を観て就寝。朝方いきなり涼しくなる。
8:15 起床。服がないので洗濯をする。 テレビのワイドショー番組を観つつ朝飯。納豆とレーズンロール。
9:00 PC をいじることにする。地獄の伯爵令嬢のボスラッシュで洗濯待ち。
11:05 ボス 11 連戦ノーセーブ荒行終了。最後は結果的にサンダーコール頼みになってしまう。 ラスボス戦の脇にワラワラ側近?が出てくる絶望感がいい。
麻雀のコードを書く。まだまだゲームにならない。 13:00 気分転換にグングニルを即死攻撃不使用で倒して外出。
13:50 ビッグエー墨田業平店。219 円。ポテチが 20 パー増量で助かる。
- ふっくらおむすび明太マヨ
- ポテチコンソメ
- あんパン
横川コミュニティー会館図書室。朝刊と教科書。カイ自乗検定の入口。
ハローワーク墨田。検索結果が不作。ブラウザーの謎アシスト機能で遊ぶ。
タイトー F ステーションオリナス錦糸町店。MJ に 5 クレ突っ込む。 最後のゲームの私のラス親という大事な局面で、あの么九牌が押し寄せてくるツモは許せない。
【SCORE】
合計SCORE:+15.9
【最終段位】
四人打ち段位:雷神 幻球:4
【7/29の最新8試合の履歴】
1st|*--*--*-
2nd|----**--
3rd|-**-----
4th|-------*
old new
【順位】
1位回数:3(25.00%)
2位回数:2(16.67%)
3位回数:5(41.67%)
4位回数:2(16.67%)
平均順位:2.50
プレイ局数:52局
【打ち筋】
アガリ率:17.31%(9/52)
平均アガリ翻:3.00翻
平均アガリ巡目:12.89巡
振込み率:9.62%(5/52)
【7/29の最高役】
・跳満
19:15 カスミオリナス錦糸町店。287 円。豚キムチ丼。
19:40 ビッグエー墨田業平店。317 円。
- スライスチーズ (5)
- 下町風のミートソース
- 小粒納豆 (3)
19:50 向島の部屋に戻る。テレビを点けて晩飯にする。 課長バカ一代の前に放送しているプリキュアに初代が出演していて感動する。
PC で帳簿をつけて電話ボックスへ移動だ。さっき確認しそびれた郵便受けをチェック。 するとおととい書類を郵送した会社のうちの一社から返信が来ている。 中を見ると面接の日程を連絡しろとある。これは今日の日中に見るべきものだった。 仕方がないので明日にする。日程の第一希望が明日なのがどうにもすっきりしない。
20:45 電話ボックスでメールもチェック。別の会社からは不採用通知。それはそうだ。 ウェブを見て回って部屋に戻る。風呂に入る。21:30 席に着く。 書類整理と復習など。
22:50 ノートを見直し終わる。SciPy の chi2 の使い方がわかったのでよしとする。
残り時間は遊ぶ……。
24:00 ある日~のレベル上げ。ついに 40 まで来た。ラストは経験値 12 万も要るのか。
Math Notes
今日は $\chi^2$ 分布を習う。まずは準備から。
確率変数 $X$ が標準正規分布 $N(0, 1)$ に従うとし、確率密度関数を $f(x)$ とおく。 $Z = X^2$ の確率密度関数を $T_1(z)$ とおくと、それは次で表されることを以下説明する。
\[\begin{aligned} T_1(z) = \begin{cases} \dfrac{1}{\sqrt{2\pi}}z^{-1/2}\mathrm{e}^{-z/2}, & z \gt 0,\\ 0, & z \le 0. \end{cases} \end{aligned}\]それはなぜか。まず $X = \pm\sqrt{Z}$ であることは次と同値である:
\[\begin{aligned} &\iff P(z\!\lt\!Z\!\lt\!z + \varDelta z) = P(x\!\lt\!X\!\lt\!x + \varDelta x) + P(-x - \varDelta x\!\lt\!X\!\lt\!-x)\\ &\iff \int_z^{z + \varDelta z}\!g(t)\,\mathrm dt = \int_{x}^{x + \varDelta x}\!f(s)\,\mathrm ds + \int_{-x - \varDelta x}^{-x}\!f(s)\,\mathrm ds. \end{aligned}\]右辺の第二項の定積分で $u = -s$ などと置換すると:
\[\begin{aligned} \int_z^{z + \varDelta z}\!g(t)\,\mathrm dt = \int_{x}^{x + \varDelta x}\!(f(s) + f(-s))\,\mathrm ds. \end{aligned}\]$s \gt 0$ とすると $\dfrac{\mathrm{d}x}{\mathrm{d}z} = \dfrac{1}{2\sqrt{z}}$ だから
\[\def\f{ \frac{1}{\sqrt{2\pi} }\mathrm{e}^{-z/2} } \begin{aligned} g(z)\,\mathrm dz &= (integrand)\,\mathrm dx.\\ \therefore g(z) &= (integrand)\frac{\mathrm{d}x}{\mathrm{d}z}\\ &= \frac{1}{2\sqrt{z}}(f(z) + f(-z))\\ &= \frac{1}{2\sqrt{z}}\left(\f + \f\right)\\ &= \frac{1}{\sqrt{2\pi z}}\mathrm{e}^{-z/2}\quad(z \gt 0). \end{aligned}\]次に確率変数 $X_1, X_2$ が互いに独立でそれぞれ $N(0, 1)$ に従うとき $Z = X_1^2 + X_2^2$ が従う分布 $T_2(z)$ を求める。 これは畳み込み積分で表される。$y \le 0 \implies T_1(y) = 0$ を利用して:
\[\def\tee#1{ \frac{1}{\sqrt{2\pi} } {#1}^{-1/2} \mathrm{e}^{-{#1}/2} } \begin{aligned} T_2(z) &= \int_0^z\!T_1(z - y)T_1(y)\,\mathrm dy\\ &= \int_0^z\! \tee{(z - y)}\cdot\tee{y}\,\mathrm dy\\ &= \frac{1}{2\pi}\mathrm{e}^{-z/2}\int_0^z\!(z - y)^{-1/2}y^{-1/2}\,\mathrm dy. \end{aligned}\]ここで $t = y/z$ と置換すると $\mathrm dy = z\,\mathrm dt$ で
\[\begin{aligned} T_2(z) &= \frac{1}{2\pi}\mathrm{e}^{-z/2}\int_0^1\!(1 - t)^{-1/2}t^{-1/2}\,\mathrm dt\\ &= \frac{1}{2\pi} \mathrm{e}^{-z/2} B\!\left(\frac{1}{2},\:\frac{1}{2}\right)\\ &= \frac{1}{2\pi} \mathrm{e}^{-z/2} \frac{\varGamma(1/2)\varGamma(1/2)}{\varGamma(1)}\\ &= \frac{1}{2\pi} \mathrm{e}^{-z/2} \cdot \pi\\ &= \frac{1}{2}\mathrm{e}^{-z/2}. \end{aligned}\]一般に $n$ 個の互いに独立な確率変数 $X_1, \dotsc, X_n$ がそれぞれ $N(0, 1)$ に従うとき $Z = X_1^2 + \dotsb + X_n^2$ の従う分布 $T_n$ は次で与えられることが数学的帰納法で証明される:
\[\begin{aligned} T_n(z) = \frac{1}{2^{n/2}\varGamma(n/2)}z^{(n - 2)/2}\mathrm{e}^{-z/2}, \quad z \gt 0. \end{aligned}\]この $T_n(z)$ の分布を自由度 $n$ の $\chi^2$ 分布という。
標本抽出に話を戻すとこう言える: $N(0, 1)$ に従う正規母集団から大きさ $n$ の標本 $X_1, \dotsc, X_n$ を無作為抽出するとき、 $X \coloneqq \sum X_i^2$ は自由度 $n$ の $\chi^2$ 分布に従う。
例:標本 $X_1, \dotsc, X_6$ を無作為抽出して $X = \sum X_i^2$ が $2.2$ を超える確率を求める。
解:次の $\alpha$ を求めろという問題である:
\[P(X\!\gt\!2.2) \gt \alpha\]$X$ は自由度 $6$ の $\chi^2$ 分布に従う。付録の表をルックアップして $\alpha = 0.900$ のところで $t = 2.20$ が現れるので、この $\alpha$ が解である。
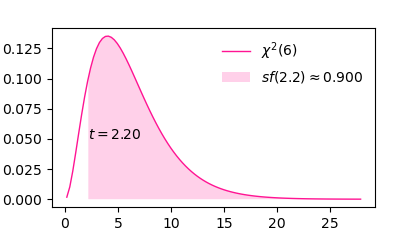
Python で計算するなら SciPy があるといい。scipy.stats は教科書に出てくる確率分布を網羅している。
今回は chi2 を採用する。
>>> from scipy.stats import chi2
>>> chi2.sf(2.2, 6)
0.9004162814033052
メソッド sf(t, ...) の戻り値は 1 - cdf(t, ...) のそれと同値である。
つまり、区間 ${(t, \infty)}$ における $\chi^2$ 分布関数の曲線と横軸との間の面積を意味する。
教科書の数表はこの右側面積の値である。
$\blacksquare$
正規母集団が $N(\mu, \sigma^2)$ に従う場合は
\[\begin{aligned} Z = \frac{1}{\sigma^2}\sum(X_i - \mu^2) \end{aligned}\]が $T_n(z)$ に従う。それはなぜか。$Z_i \coloneqq \dfrac{X_i - \mu}{\sigma}$ が $N(0, 1)$ に従うことによる。
例:$N(3, \sigma^2)$ に従う正規母集団から $n = 12$ 個の標本を無作為抽出する。 $X \coloneqq \sum(X_i - 3)^2$ について $P(X\gt48) \gt 0.1$ なる $\sigma$ はいくつか。
解:$Z \coloneqq X/\sigma^2$ は自由度 $12$ の $\chi^2$ 分布に従う。
>>> chi2.isf(0.1, 12)
18.54934778670325
>>> sigma_sq = 48 / _; sigma_sq
2.587692060763877
メソッド isf() は sf() の逆関数である。単調減少関数の逆関数なので単調増加である。
曲線と座標軸に囲まれた面積(右側)から対応する座標を返す。
上のコードでは自由度 $12$ の $\chi^2$ 分布曲線に対する $z = 18.5493…$ の右側の面積が $0.1$ になることを示している。
$\blacksquare$
$N(\mu, \sigma^2)$ に従う正規母集団から $X_1, \dotsc, X_n$ を無作為抽出して
\[\begin{aligned} \bar{X} = \sum X_i \end{aligned}\]をつくると
\[\begin{aligned} Z \coloneqq \frac{1}{\sigma^2}\sum(X_i - \bar{X})^2 = \frac{nS^2}{\sigma^2} \end{aligned}\]は自由度 $n - 1$ の $\chi^2$ 分布に従う。
例:さきほどの例で $\mu$ を未知として $P(S^2 \gt 4.0) \gt 0.1$ となる $\sigma^2$ はいくつか。
解:$S^2 = 4.0$ であることと $X = 48$ が対応する。 $Z \coloneqq 12S^2/\sigma^2$ は自由度 $n = 11$ の $\chi^2$ 分布に従う。
>>> chi2.isf(0.1, 11)
17.275008517500076
>>> 12 * 4.0 / _
2.7785803955682353
前問のコメントを参照。 $\blacksquare$
最後に、$Z \coloneqq \dfrac{n}{\sigma^2}(\bar{X} - \mu)^2$ は自由度 $1$ の $\chi^2$ 分布に従う。
$\chi^2$ 分布も正規分布と同様に重ね合わせの原理が成り立つ。
以上