97 日目(曇のち晴れ)都バス・地下鉄がフリーライドになる
よく憶えていないがブリューゲルの息子のほうの絵が画面に映っていたと思う。寝る。
9:00 起床。きのうはさすがに疲れた。ホームレスのときでもこんなに疲れた日はまれだった。 朝飯は納豆とレーズンロール。衣類洗濯日とシーツ洗濯日が重なるのを避けるため、服をきょう洗うことにする。
洗濯が終わるまで PC をいじる。麻雀の練習とレベル上げ。洗濯物を干して出かける準備。
10:45 外出? せっかく謎乗車券を入手したので八広方面に都バスで行くのも一興と思いバス通りへ。 しかしこの通りのバスは南千住行きで、曳舟あたりで北上してしまうようだ。 結局徒歩でいつものルートを移動することにする。途中の公園で水浴び&水補給。
11:45 八広図書館に到着。殺風景になったロビーで朝刊を読みふけってから入館。 線路寄りのキャレルで持参 PC をいじる。ここは冷風がガンガン来て天国だ。 帰りにマックファンを読む。鈴木みそ先生の小池百合子閣下のマンガが実質目しか描かれていないのにそっくりですごい。
13:30 退館。都バス通りへ自然に足が向かう。なぜか何食べを読む。
13:50 ビッグエー墨田八広店。223 円。
- ふっくらおむすび各種 (2)
- すっぱムーチョさっぱり梅
隣の公園(名前忘れた。前作ブログに記載あり)でおやつ休憩。
14:20 頃に都バス錦糸町駅前行きに乗車。謎乗車券は見せるだけでいいのか。 楽をさせてもらいつつ横尾川三丁目で降車。いや本当に楽だ。
横川コミュニティー会館図書室に移動して週刊新潮のバックナンバーと教科書を読む。
タイトー F ステーションオリナス錦糸町店。またぞろ 6 クレ使ってしまう。 ビートマニアの ARENA はムリヤリ B2 まで来たものの、人間と当たるとまず勝てない。出直しだ。
MJ プロ卓東風戦。なかなかトップが獲れなくて長引く。まあいいや。
【SCORE】
合計SCORE:+1.9
【最終段位】
四人打ち段位:雷神 幻球:6
【8/1の最新8試合の履歴】
1st|-----**-
2nd|-*--*--*
3rd|*-*-----
4th|---*----
old new
【順位】
1位回数:2(16.67%)
2位回数:5(41.67%)
3位回数:3(25.00%)
4位回数:2(16.67%)
平均順位:2.42
プレイ局数:56局
【打ち筋】
アガリ率:23.21%(13/56)
平均アガリ翻:2.85翻
平均アガリ巡目:10.92巡
振込み率:7.14%(4/56)
【8/1の最高役】
・倍満
・跳満
18:45 カスミオリナス錦糸町店。319 円。のりチキン竜田弁当。
19:15 けっきょく徒歩でビッグエー墨田業平店まで移動。273 円。
- エクレア
- 小粒納豆 (3)
- 絹豆腐 (3)
- レーズンロール (4)
やはり歩きで向島の部屋に戻る。たぶん日暮里駅行きのバスに乗ればいいのだと思うが、タイミングが合わない。 とにかく晩飯にする。カネオくんを観ながら帳簿をつけたら 20:00 を回る。
いちおう電話ボックスへ移動してインターネット作業をする。涼しいので長めに作業できるときに限って何もないとは。 いや、都バスの路線図が欲しい。しかしデータがない?
部屋に戻って風呂。上がって PC 作業。数学をやる。
22:30 復習終わり。最後の問題はオリジナル通りに $5\%$ で計算すると $F$ 分布と $t$ 分布とで答えが入れ替わるのでおかしい。明日見直す。 見直した。原因は $t$ 分布の偶関数性にあった。$F$ のときの面積を半分にして(平方根をとる)と釣り合う。 だから解答は正しい。
もう一回フリーリ戦をやる。脇に出てくるザコがどれだけ用意されているのか調べる。 しかし知っている 4 体で打ち止めのようだ。 ネコとか出てきたら投げていたかもしれない。レベルを 1 だけ上げて終わる。
麻雀の練習をやって消灯に入る。
Math Notes
今日は $t$ 分布。これは自由度 $(1, n)$ の $F$ 分布、
\[\begin{aligned} f_{1, n}(x) &= \frac{n^{\frac{n}{2}}x^{-\frac{n}{2}}}{B(1/2, n/2)(x + n)^{\frac{1 + n}{2}}}, & x \gt 0, \end{aligned}\]において $X = T^2$ と変数変換をするときの $T = t$ の従う分布 $f_n(t)$ のことをいう。
その $f_n(t)$ とは次のように求める。まず平方変換の分布は次のものだと習った:
\[\begin{aligned} f_{1, n}(x) &= \frac{1}{2\sqrt{x}}(f_n(x) + f_n(-x)), & t = \pm\sqrt{x}. \end{aligned}\]$f_n(t)$ が偶関数であると仮定すると、
\[\begin{aligned} f_{n}(x) &= \sqrt{x}f_{1, n}(x)\\ &= \frac{n^{\frac{n}{2}}}{B(1/2, n/2)(x + n)^{\frac{1 + n}{2}}}\\ &= \frac{n^{-\frac{n}{2}}}{B(1/2, n/2)}\left(\frac{n}{x^2 + n}\right)^{\frac{n + 1}{2}}\\ &= \cfrac{1}{\sqrt{n}B\!\left(\dfrac{1}{2}, \dfrac{n}{2}\right)\!\left(1 + \dfrac{t^2}{n}\right)^{\frac{n + 1}{2}}}. \end{aligned}\]これを自由度 $n$ の $t$ 分布 a.k.a. Student 分布という。
巻末の数表としては $\displaystyle \int_t^\infty f_n(x)\,\mathrm dx = \dfrac{\alpha}{2}$ のものが掲載されている。分布が偶関数であることに注意。
もう一度言うが $t$ 分布は自由度 $(1, n)$ の $F$ 分布と本質的には変わらない。 そこで前回の命題を $t$ 分布で言い換えることができる:
-
$N(\mu, \sigma^2)$ に従う正規母集団から大きさ $n$ の標本を無作為抽出して標本平均 $\bar{X}$ と標本分散 $S^2$ を計算する。このとき
\[\begin{aligned} \pm\sqrt{X^2} = T = \frac{\sqrt{n - 1}(\bar{X} - \mu)}{S} \end{aligned}\]は自由度 $n - 1$ の $t$ 分布に従う。
-
母分散の等しい二つの正規分布 $N(\mu_x, \sigma^2), N(\mu_y, \sigma^2)$ にそれぞれ従う母集団からそれぞれ大きさ $m, n$ の標本を無作為抽出して標本平均と標本分散 $\bar{X}, \bar{Y}, S_x^2, S_y^2$ を計算する。このとき
\[\pm\sqrt{X^2} = T = \frac{\sqrt{m + n - 2}((\bar{X} - \bar{Y}) - (\mu_x - \mu_y))}{\sqrt{(1/m + 1/n)(mS_x^2 + nS_y^2)}}\]は自由度 $m + n - 2$ の $t$ 分布に従う。
例:母平均 $\mu = 6.3$ の正規母集団から $20$ 個を無作為抽出して標本を作る。 標本平均、標本分散をそれぞれ計算すると $\bar{X} = 8.2,\;S^2 = 12.6$ であった。 このような結果が生じる確率は $1\%$ より小さいか大きいか。
解:おとといの日記の問題そのものだ。これを $t$ 分布で解く。
\[T = \sqrt{X} = 2.33316325...\]手許に数表がないので Python を使う。サードパーティーパッケージ SciPy が必須。
>>> from math import sqrt
>>> from scipy.stats import t
>>> t.isf(0.01 / 2, 20 - 1)
2.860934606449914
>>> sqrt((20 - 1) * (8.2 - 6.3)**2 / 12.6)
2.3331632591078555
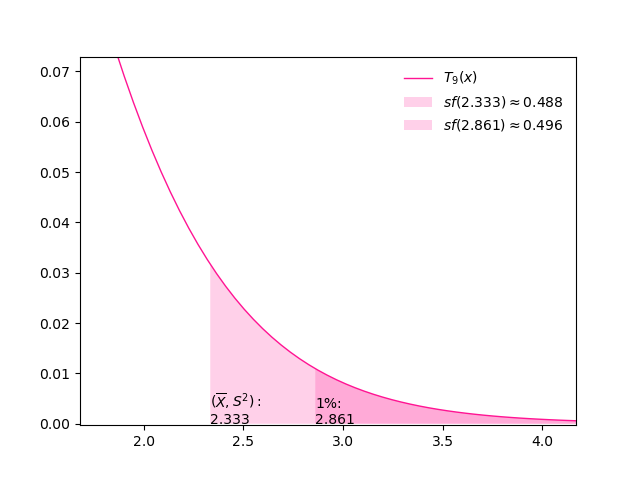
上のプロットは紙幅の都合上正の部分しか描いていないが、負の部分にももちろんある。
理屈は先日までの学習と同じだ。 $-2.860… \lt 2.333… \lt 2.860…$ だから $1\%$ より大きいと言える。 $\blacksquare$
問:母平均のわからぬ正規母集団から標本を $9$ 個無作為抽出して標本分散 $S^2$ を計算する。これを繰り返す。$5\%$ の確率で $S^2 \gt 1.0$ となる母分散 $\sigma^2$ はいくらであるか。
解:$nS^2/\sigma^2$ は自由度 $n - 1 = 8$ の $\chi^2$ 分布に従う。
>>> from scipy.stats import chi2
>>> chi2.isf(0.05, 9 - 1)
15.507313055865454
>>> 9 * 1.0 / _
0.5803713362577573
上記計算によると $\sigma^2 = 0.580…$ である。 $\blacksquare$
問:母分散の等しい二つの正規母集団から、一方は $4$ 個、他方は $7$ 個の標本を無作為抽出して $S_x^2, S_y^2$ を標本分散としてそれぞれ計算する。すると前者は後者のちょうど $10$ 倍であった。 このようになる確率は $1\%$ より大きいか小さいか。
解:自由度 $(3, 6)$ の $F$ 分布に従う。
\[\begin{aligned} X = \frac{4\cdot(7 - 1)\cdot10 S_y^2}{7\cdot(4 - 1)\cdot S_y^2} = 12.5 \end{aligned}\]>>> from scipy.stats import f
>>> X = 4 * (7 - 1) * 10 / (7 * (4 - 1)); X
11.428571428571429
>>> f.isf(0.01, 3, 6)
9.779538240923273
$P(X \gt 9.779…) = 0.01$ だから $1\%$ より低い確率であると言える。 $\blacksquare$
例:$N(2.0, 8)$ に従う母集団から $5$ 個無作為抽出すると $\bar{X} = 5.3,\;S_x^2 = 12$ であった。また $N(3.5, 8)$ に従う母集団から $6$ 個無作為抽出すると $\bar{Y} = 2.1,\;S_y^2 = 10$ であった。
このようなことが起こる確率は $10\%$ より小さいか大きいか。 $t$ 分布を使って求めろ。
解:$P(\lvert T \rvert \gt 1.8331…) = 0.1.$ を確かめる:
>>> t.isf(0.1 / 2, 9)
1.8331129326536337
>>> sqrt(5 + 6 - 2)*((5.3 - 2.1) - (2.0 - 3.5))/sqrt((1/5 + 1/6)*(5*12 + 6*10))
2.125654979273233
$T = 2.1256… \gt 1.8331…$ であるから $10\%$ より小さいと言える。 $\blacksquare$
以上