5:30 Ｋ公園ベンチで起床。周りの会話で目が覚める。それによると今日は雨が降るらしい。となると中央図書館方面へ移動したほうがいい。早速移動開始。

6:30 中央公園（北）へ到着。途中、南大橋下の児童遊園で体操をしているおばさんを見かけた。 私が寝泊まりしてそこに居座っている日には、敬遠して体操をしていない可能性も考慮するか。

本当に雨が降ってきたので図書館の駐輪所軒下に避難。 リュックに入っている牛乳、リンゴパン、バターロールを食べる。

瞑想などをして時間を潰し、9:00 北区中央図書館館内に入場。 IPython をいじりながら数論の教科書の練習問題に取り組む。反則ではないのだ。

14:00 サミット滝野川紅葉橋店でおやつを買い食い。メロンパンと柿ピーで腹をふくらませる。

17:00 祝日につき図書館閉館。おん出て赤羽方面に徒歩で移動。意外に蒸し暑い。 赤羽公園のキリン前ベンチでさっき解けなかった練習問題を考える。

結局解けず晩飯に逃げることにした。19:30 西友赤羽店でアジフライ、おにぎり、玉ねぎのみじん切りサラダを買って食う。

残り時間はゲーセン。ノスタルジアは秋の演奏会が終わりそうにない。確か今週中に新作が入るはず。

MJ で面白い一局があった。タンヤオを狙ったらなぜか三槓子を聴牌した。 展開は正確には記憶していないが、加槓、暗槓、大明槓すべてのカンを達成して手配が暗刻プラス単騎の形になった。 暗刻の牌の残りが私には見えていないので、四槓子聴牌まで期待できる胸の熱い事態になった。 単騎は生牌の北。他家は全員最強位なので、流局確定みたいなもの。 実際流局し、北は両脇に抑えられていた。今日はこれだけで満足だ。

今晩は食料を調達せず就寝。

読み物

  • 朝日新聞朝刊
  • 産経新聞朝刊
  • ふらんす 2018.10 号
  • 鈴木治郎訳『はじめての数論 原著第 3 版』

『はじめての数論』練習問題 21.7. <100 より小さいすべての素数について原始根が 3 であるものを見つけよ> を目的をコードの形式ではっきりさせておく：

>>> from math import gcd
>>> from sympy.ntheory import n_order, totient, is_primitive_root

>>> [p for p in primerange(2, 100) if gcd(3, p) == 1 and n_order(3, p) == totient(p)]
... [2, 5, 7, 17, 19, 29, 31, 43, 53, 79, 89]

>>> [p for p in primerange(2, 100) if gcd(3, p) == 1 and is_primitive_root(3, p)]
... [2, 5, 7, 17, 19, 29, 31, 43, 53, 79, 89]

ただし n_order を実装することに相当する問題が 21.10. だ。

Python

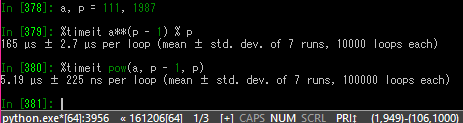
標準関数 pow にはオプショナルな第 3 パラメーターがあり、それはべき乗の剰余を得るのに利用できる。

from sympy.ntheory import factorint

primes = (3, 5, 7, 11)

for p in primes:
    factors = factorint(p - 1)
    for i in factors.keys():
        assert pow(i, p - 1, p) == 1

効率が演算子を組み合わせるよりも段違いに優っている。

Python integrated function pow