第 4 章 微分形式とベクトル場 3/4¶
4.3 接平面場(展開)¶
4.3.1 フロベニウスの定理¶
接平面場 or 接分布 を余接空間と接空間の関係で定義する。
\({\alpha \in \varOmega^1(M)}\) と \({x \in M}\) に対して \({\ker\alpha} = \set{v \in T_xM \sth \alpha(v) = 0}\) は接空間 \(T_xM\) の \({\dim M - 1}\) 次元部分多様体である。
対応 \({x \longmapsto \ker\alpha}\) による \(TM\) の部分ベクトル束を 接平面場 or 接分布 と呼ぶ。
一般には各点 \({x \in M}\) に接空間 \(T_xM\) の \(r\ {(r \le \dim M)}\) 次元部分空間を対応させる写像を接平面場 or 接分布と呼ぶ。
関数 \({f \in \varOmega^0(M)}\) が点 \({x_0 \in M}\) において \({\dd f \ne 0}\) であるとする。
このとき部分集合 \(\set{x \in M \sth f(x) = f(x_0)} \subset M\) は点 \({x_0 \in M}\) の近傍で \({\dim M - 1}\) 次元部分多様体である。
この近傍は \({\dim M - 1}\) 次元の等位面で埋め尽くされていて、
\({\ker\dd f}\) は各点で等位面の接空間と一致する。
1 形式 \({g {\dd f} \in \varOmega^1(M)}\) が点 \({x_0 \in M}\) で \({g(x) \ne 0}\) であるとする。このとき、状況は上記と同様になる。
1 形式 \({\alpha = {g\dd f} \in \varOmega^1(M)}\) が点 \({x_0 \in M}\) の近傍で \({\alpha \ne 0}\) であるとするならば、\(\alpha \wedge {\dd \alpha} = 0\) が成り立つ。
\({\alpha \wedge \dd \alpha} = {g\,\dd f} \wedge {(\dd f \wedge \dd f)} = 0\) による。
定理 4.3.1: 上の逆が成立する
\({\alpha \in \varOmega^1(M)}\) が点 \({x_0 \in M}\) の近傍で \({\alpha \ne 0}\) であり、
\({\alpha \wedge \dd \alpha = 0}\)
ならば、点 \({x_0 \in M}\) の近傍の関数 \(f, g\) が存在して、 \({\alpha = g\,\dd f}\) が成り立つ。
証明をするための多様体上の点と座標近傍、微分形式、枠場を設定する:
\({x_0 \in (U, \varphi = (x_1, \dotsc, x_n))}\)
\(\displaystyle \alpha = \sum_{i = 1}^n {f_i\,\dd x_i} \in \varOmega^1(M)\), ただし \(f_n = 1\)
\(\xi_i = \dfrac{\partial}{\partial x_i} - f_i{\partial}{\partial x_n}\quad{(i = 1, \dotsc, n - 1)}\)
\({\alpha \wedge \dd\alpha = 0}\) であるので、次のようになっている:
\[0 = \sum_i\sum_k\sum_j f_i \dfrac{\partial f_k}{\partial x_j}\,\dd x_i \wedge \dd x_j \wedge \dd x_k.\]括弧積を定義に従って計算すると次のようになる:
\[[\xi_i, \xi_j] = \left( \dfrac{\partial f_j}{\partial x_i} +\dfrac{\partial f_i}{\partial x_j} + f_i \dfrac{\partial f_j}{\partial x_n} - f_j \dfrac{\partial f_i}{\partial x_n} \right) \dfrac{\partial}{\partial x_n}.\]ここで 2. の和のうち \({\dd x_i} \wedge {\dd x_j} \wedge {\dd x_n}\) の係数は 3. の括弧内のものと等しい。したがって 3. の値はゼロである。
以上より、\(\xi_1, \dotsc, \xi_{n - 1}\) は、
生成するフローが可換であり、
\(\RR^{n - 1}\) の局所的な作用を生成し、
\({\ker\dd f}\) を張る
\(\varphi\inv{(0, \dotsc, 0, f(x))}\) がどうのと言っている。
ベクトル場である。幾何学 I 8.4 節 を参照。
各点 \({x \in M}\) で、\(\alpha\) は \({\dd f}\) のゼロでない関数倍である。つまり \({\alpha = g}\,{\dd f}\) なる \({g \ne 0}\) が存在する。
定理 4.3.1 の条件を満たす接平面場と定理 4.3.1 の関数 \(f\) の等位面の接平面場は同じもの(局所的)。これを「多様体 \(M\) に余次元 1 葉層構造 が与えられている」という。
葉層構造の定義はこういう感じだ:
\(n\) 次元多様体の弧状連結部分集合族 \(\set{L_i \sth i \in I}\) が葉層構造であるとは、以下を満たすことをいう:
\({i, j \in I}, {i \ne j} \implies {L_i \cap L_j = \varnothing.}\)
\({\bigcup_{i \in I} L_i = M.}\)
\({x \in M}\) の座標近傍 \({(U, \varphi)}\) において \({U \cap L_i \subset M}\) が \(M\) の部分多様体である。この部分多様体の余次元が葉層構造の余次元として定義される。
関数の等位面をつなぎ合わせると \(\dim M - 1\) 次元部分多様体が定義される(局所的)。
この部分多様体の極大なものを 葉 という。
上の定義でいうところの各 \(L_i\) だ。
例えば任意の接ベクトル \({v \in T_xM}\) に対して \({\alpha(v) \ne 0}`なる :math:`{\alpha \in Z^1(M)}\) は定理 4.3.1 の仮定を満たすので、余次元 1葉層構造がある。
微分形式が閉形式であるというのがありがたい。
\({\alpha = g}\,{\dd f}\) が点 \({x_0 \in M}\) の近傍でゼロでなければ、\({\dd\alpha} = {\dd f \wedge \dd f} = {\dfrac{1}{g} \wedge \alpha}\) と書ける。よって、\({\alpha \wedge \dd\alpha = 0}\) ならば、\({\beta \in \varOmega^1(M)}\) が存在して \({\dd\alpha = \beta \wedge \alpha}\) が成り立つと言い変えてもよい。
命題 4.3.2: 1 形式と \(p\) 形式の外積に対する \(p - 1\) 形式の存在
\({\alpha \in \varOmega^1(M)},\ {\alpha \ne 0}\)
\({\beta \in \varOmega^p(M)}\)
\({\alpha \wedge \beta = 0}\)
ならば、\({\exists \gamma}\quad\text{s.t. }{\beta = \gamma \wedge \alpha.}\)
余接空間 \(T_x^*M\) の基底を \(\dd x_1, \dotsc, \dd x_n\) から \(e_1, \dotsc, e_n\) に取り替えることを考える。ここで \({\alpha(x) = e_1}\) とする。
同時に \(\extp^p {T_x^*M}\) の基底も \({\dd x_{i_1}} \wedge {\dd x_{i_p}}\) から \(e_{i_1} \wedge e_{i_p}\) に置き換わる。
この取り替えは点 \({x \in M}\) の座標近傍 \({(U, \varphi)}\) で各 \(e_i\) が \(C^\infty\) 級写像となるようにとれる。
\(\displaystyle {\alpha = e_1}, {\beta = \sum_{j_1 \lt \dotsb j_p}g_{j_1 \dots j_p}e_{j_1} \wedge \dotsb {\wedge e_{j_p}}}\) と書ける:
\({\alpha \wedge \beta = 0}\) より \({1 \lt j_1}\) ならば \({g_{i_1 \dots i_p} = 0}\) である。したがって次が成り立つ:
\[\beta = \sum_{j_2 \lt \dotsb j_p}g_{1 j_2 \dots j_p}e_{j_2} \wedge \dotsb \wedge e_{j_p}.\]\(M\) の開被覆 \(U_i\) を 2. のようにとり、これに従属する 1 の分割 \(\lambda_i\) をとる。
\({\exists \gamma_i \in \varOmega^{p - 1}(U_i)}\quad\text{s.t. }{\beta = \alpha \wedge \gamma_i.}\)
\({\gamma = \sum\lambda_i\gamma_i}\) に対して:
\[\begin{split}\begin{align*} \alpha \wedge \gamma &= \alpha \wedge \sum_i \lambda_i\gamma_i\\ &= \sum_i \lambda_i\alpha_i \wedge \gamma_i\\ &= \sum_i \lambda_i\beta\\ &= \beta. \end{align*}\end{split}\]
これは 定理 4.3.1 の言い換えである。
次のテーマは写像 \(\fn{F}{U}\RR^q\) で定まる多様体の族である。
\({\rank F = q}\) とする。このとき座標 \(\fn{\varphi}{U}\RR^n\) で \(F\) が射影 \({\RR^n \longto \RR^q}\) に一致するものがうまくとれる。
射影でない方の座標を \({(x_1, \dotsc, x_p)}\)
射影のほうを \({(y_1, \dotsc, y_q)}\)
とすると、部分多様体の接空間は次で与えられる:
\[\ker\dd y_1 \cap \dotsb \cap \ker\dd y_q.\]行列による線形写像 \(\displaystyle \fn{A = (a_{ij})}{U}GL_q(\RR)\) と 1 形式 \({\alpha_i = \sum_{i = 1}^q a_{ij}\,{\dd y_j}\quad{(i = 1, \dotsc, q)}}\) を考えると、部分多様体の族の接空間は次で与えられる:
\[\ker\alpha_1 \cap \dotsb \cap \ker\alpha_q.\]この 1 形式に対する外微分を計算する:
\[\begin{split}\begin{align*} \dd\alpha_i &= \sum_{i = 1}^q \dd a_{ij} \wedge \dd y_j\\ &= \sum_{i = 1}^q \dd a_{ij} \wedge \left(\sum_{k = 1}^q(A\inv)_{jk}\alpha_k\right)\\ &= \sum_k\left(\sum_j (A\inv)_{jk}\,\dd a_{ij}\right) \wedge \alpha_k \end{align*}\end{split}\]つまり \({\beta_{ik} \in \varOmega^1(U)}\) が存在して \({\dd \alpha_i} = \sum {\beta_{ik} \wedge \alpha_k}\) と書けることを意味する。これを 完全積分可能条件 という。
厳密に言うと上記「つまり~」以降は積分可能条件と呼ばれるらしい。本書での多様体は滑らかな多様体であるため、完全積分可能条件と自動的に一致するというのが本当らしい。
問題 4.3.3: 上記の存在条件は \(\alpha_i\) のとり方に依存しない
示すべきは \({\ker\alpha_1 \cap \dotsb \cap \ker\alpha_q} = {\ker\alpha'_1 \cap \dotsb \cap \ker\alpha'_q}\) と書けるときに、 \(\displaystyle {\alpha'_i = \sum_{j = 1}^q a'_{ij}\alpha_j}\) となるような \(\fn{A' = (a'_{ij})}{U}GL_q(\RR)\) が存在することを使って \(\displaystyle {\dd \alpha'_i} = \sum_{i = 1}^q {\beta'_{ik} \wedge \alpha'_k}\) なる \({\beta'_{ik} \in \varOmega^1(U)}\) があることだ。
定理 4.3.4: フロベニウスの定理
多様体 \(M^{p + q}\) の各点において近傍 \({U \subset M}\) が存在して、
\(\alpha_1, \dotsc, \alpha_q \in \varOmega^1(U)\) が一次独立で、
\({\ker\alpha_1 \cap \dotsb \cap \ker\alpha_q}\) で \(p\) 次元接平面場が表される
とする。この接平面場が点の近傍 \(V \subset\) からユークリッド空間へのランク \(q\) の写像 \(\fn{F}{V}\RR^q\) で定まる \(p\) 次元部分多様体の族の接平面場となることと、次が同値となる:
\[\exists \beta_{ik} \in \varOmega^1(V)\quad\text{s.t. } \dd\alpha_i = \sum_{k = 1}^q \beta_{ik}\wedge\alpha_k.\]\(\Longleftarrow\) 側の証明が残っている。
座標近傍 \({(U, \varphi = (x_1, \dotsc, x_p, y_1, \dotsc, y_q)}\) において \(p\) 次元接平面場は射影に対して横断的であるとする。
接平面場は次の \(p\) 個のベクトル場が張る:
\[\xi_i = \dfrac{\partial}{\partial x_i} + \sum_{l = 1}^q b_{li}\dfrac{\partial}{\partial y_l}.\]必要なら各 \(\alpha_l\) を並び替えて次が成り立つようにする:
\[\alpha_l = \dd y_l = \sum_{i = 1}^p b_{li}\,\dd x_i.\]このとき各微分形式の核の共通部分は保たれる。
\(F\) で定まる \(p\) 次元部分多様体の族の接平面場となるとき、2. のベクトル場が局所的に生成するフローは可換である。
ベクトル場が \(p\) 次元部分多様体の接空間に接しているので、 \({[\xi_i, \xi_j]}\) はそこに値を持つ。それゆえ \(\displaystyle {[\xi_i, \xi_j]} = \sum_{i = 1}^p {c_i\xi_i}\) のように線形結合の形で書けるはずだが、左辺の \(\dfrac{\partial}{\partial x_i}\) の各成分はゼロであり、したがって全体としてゼロである。
ベクトル場 \(\xi\) が可換である条件を計算で求める。
\(\alpha_l\)
\(\displaystyle {\dd\alpha_l} = \sum_{k = 1}^q{\beta_{ik}\wedge \alpha_k}\)
\(\displaystyle \beta_{li} = \sum_{j = 1}^p f_{lij}\,{\dd x_j} + \sum_{j = 1}^q g_{lij}\,{\dd y_j}\)
を利用して条件を詰めていく。難しい。
\(\displaystyle {[\xi_i, \xi_j]} = \sum_{m = 1}^q(\cdots)\dfrac{\partial}{\partial y_m}\) の形に書き換えれば、括弧内がゼロになる。
これで \(\xi_1, \dotsc, \xi_p\) が生成するフローが可換であり、 \(\RR^p\) の局所的な作用を生成することが言えた。
\(\xi_1, \dotsc, \xi_{n - 1}\) は \(F\) により定まる \(p\) 次元部分多様体の族の接平面場を張る。
問題 4.3.6: \(SL_2(\RR)\) の左不変完全積分可能二次元平面場
本問は 問題 4.2.2 (2) で途中まで計算済み。そのときの解答例の値ではなく、自分の計算結果で求めてみる。
\({\alpha = aH^* + bS^* + cU^*}\) とおいて \({\dd\alpha \wedge \alpha = 0}\) となる条件を示せばよい。
\[\begin{split}\begin{align*} \dd\alpha \wedge \alpha &= (aS^* \wedge U^* + 2b H^* \wedge S^* -2cH^* \wedge U^*) \wedge (aH^* + bS^* + cU^*)\\ &= a^2 S^* \wedge U^* \wedge H^* + 2bc H^* \wedge S^* \wedge U^* - 2bc H^* \wedge U^* \wedge S^*\\ &= (a^2 + 4bc)H^* \wedge S^* \wedge U^*\\ \end{align*}\end{split}\]であるから、\(c\) を消去すれば(しなくていいが)求める 1 形式は次の形のものだ:
\[\alpha = 4ab H^* + 4b^2 S^* - a^2 U^*.\]本問解答例 \(\alpha\) の \(S^*\) と \(U^*\) の係数がそれぞれ 2 倍だけ異なる。
問題 4.3.7: \(M\) 上の余次元 1 の接平面場が \({\alpha \in \varOmega^1(M)}\) で与えられるとする
完全積分可能条件より \({\beta \in \varOmega^1(M)}\) に対して \({\dd\alpha = \beta \wedge \alpha}\) となるものが存在する。
\({\beta \wedge \dd \beta \in Z^3(M)}\)
2. のドラーム・コホモロジー群は \(\beta\) のとり方に依存しない。
\({\dd\alpha = \beta \wedge \alpha}\) の両辺を外微分することで \({\dd\beta \wedge \alpha = 0}\) がわかる:
\[\begin{split}\begin{align*} 0 = \dd(\dd\alpha) &= \dd\beta + \alpha + \beta \wedge \dd\alpha\\ &= \dd\beta + \alpha + \beta \wedge \beta \wedge \alpha\\ &= \dd\beta + \alpha. \end{align*}\end{split}\]命題 4.3.2 より \({\dd\beta = \gamma \wedge \alpha}`をみたす :math:`{\gamma \in \varOmega^1(M)}\) があるので:
\[\begin{split}\begin{align*} \dd(\beta \wedge \dd\beta) &= \dd\beta \wedge \dd\beta + \dd(\dd\beta)\\ &= (\gamma \wedge \alpha) \wedge (\gamma \wedge \alpha) + 0\\ &= 0. \end{align*}\end{split}\]\({\dd\alpha} = {\beta \wedge \alpha} = {\beta' \wedge \alpha}\) なる \(\beta'\) をとる。このとき \({(\beta' - \beta) \wedge \alpha = 0}\) だから 命題 4.3.2 より \({\beta' - \beta = h\alpha}`を満たす :math:`h \in \varOmega^0(M)\) が存在する。
\({\beta' \wedge \dd\beta'} = {\beta \wedge \dd\beta} - {\dd(\beta \wedge (h \wedge \alpha))}\) なので、確かに \(\beta'\) のとり方に依存しない。
\(\alpha'\) を \(\alpha\) が定まる余次元 1 接平面場と同じものを定めるものとする。このとき 命題 4.3.2 の前座部分より、局所的に \({\alpha' = g\alpha\quad(g \ne 0)}\) を満たす関数 \({g \in \varOmega^0(M)}\) が存在する。
\[\begin{split}\begin{align*} \dd\alpha' &= \dd g \wedge \alpha + g \dd\alpha\\ &= \dd g \wedge \alpha + g\beta \wedge \alpha\\ &= \left(\frac{\dd g}{g} + \beta\right) \wedge (g\alpha)\\ &= (\dd\log\abs{g} + \beta) \wedge (g\alpha). \end{align*}\end{split}\]最初の等号に \({\alpha' = g\alpha}\) を使用した。
二番目の等号に 1. を使用した。
三番目の等号は左から \(\dfrac{1}{g}\) を、右から \(g\) を乗じてある。
最後の等号に対数が出てくるのは逆数の不定積分のように見える。
\[(\dd\log\abs{g} + \beta) \wedge (\dd\log\abs{g} + \beta) = \beta \wedge \dd\beta + \dd(\log\abs{g} \wedge \beta)\]となり、\(\alpha\) のとり方に依存しない。
注意 4.3.8: ゴドビヨンベイ類
4.3.2 微分形式の核¶
前節の \(\ker\alpha\) の定義を一般の \({\alpha \in \varOmega^p(M)}\) に拡張する:
これもまた線形空間になっている:
例 4.3.9:
(1) \({0 \ne \varOmega \in \varOmega^n(M^n)}\) に対しては \({\ker\alpha = 0.}\)
(2) ユークリッド空間の例。
\(T_0\RR^4\) で \({\ker(\dd x_1 \wedge \dd x_2 + \dd x_3 \wedge \dd x_4) = 0.}\)
\(T_0\RR^6\) で \({\ker(\dd x_1 \wedge \dd x_2 \wedge \dd x_3 + \dd x_4 \wedge \dd x_5 \wedge \dd x_6) = 0.}\)
問題 4.3.10: \({\alpha \in \varOmega^p(M),} {\beta \in \varOmega^q(M)} \implies {\ker(\alpha \wedge \beta) \supset \ker\alpha \cap \ker\beta}\)
証明には \({i_v\alpha = i_v\beta = 0}\) から出発して \({i_v(\alpha \wedge \beta) = 0}\) を示す。次数付き可換性を用いて式変形する。
4.3.3 体積形式とダイバージェンス¶
冒頭の微分形式 \(\varOmega\) のようなものを 体積形式 という。つまり、向き付けられた n 次元多様体 \(M\) における \({\varOmega \in \varOmega^n(M)}\) が正の局所座標系 \({(x_1, \dotsc, x_n)}\) において各点 \({x \in M}\) において
\[\varOmega = a\!\dd x_1 \wedge \dotsb \wedge \dd x_n\]と表すと \({a \gt 0}\) であるようなものだ。
ベクトル場 \(\xi\) の体積形式 \({\varOmega \in \varOmega^n(M)}\) に対する発散、\(\div\xi\) とは次の式を満たす関数である:
\[L_\xi\varOmega = (\div\xi)\varOmega.\]\({\varOmega \in \varOmega^n(M)}\) は各点で \({\ne 0}\) とする(多様体が向き付け可能であることと同値)。
\(\displaystyle \xi = \sum_i^n\xi\dfrac{\partial}{\partial x_i}\) の \({{\dd x_1} \wedge \dotsb \wedge {\dd x_n}}\) に対する発散は次のようになる:
\[\div\xi = \sum_i^n\dfrac{\partial \xi}{\partial x_i}.\]
-
向き付けられた多様体 \(M\) で使える公式である:
\[\int_M\!\div\xi\varOmega = \int_{\partial M}\!i_\xi\varOmega.\]なぜこれが成り立つのか:
\[\begin{split}\begin{align*} \int_M\!\div\xi\varOmega &= \int_M\!L_\xi\varOmega\\ &= \int_M\!\dd(i_\xi\varOmega)\\ &= \int_{\partial M}\!i_\xi\varOmega. \end{align*}\end{split}\]特に \(M\) がコンパクト閉多様体であれば、積分の値はゼロである。
注意 4.3.11: モーザーのアイソトピー
コンパクトで向き付け可能な多様体 \(M\) と、その上の微分形式 \({\varOmega_1 \ne 0,} {\varOmega_2 \ne 0}\) に対して、
\[\int_M\!\varOmega_0 = \int_M\!\varOmega_1\]が成り立つのであれば、次の条件を満たすアイソトピー \(\fn{F_t}{M}M\) が存在する:
\[F_0 = \id_M,\ F_1^*\varOmega_0 = \varOmega_1.\]
4.3.4 シンプレクティク形式とハミルトン・ベクトル場¶
問題 4.3.12: ユークリッド空間原点近傍の 2 形式の核がゼロしかないとき
\(\omega\) を \(n\) 次元ユークリッド空間の 2 形式とし、
\({\ker\omega = 0}\) であるとする。
このとき次のすべてが成り立つ:
ユークリッド空間の次元 \(n\) は偶数 \({n = 2m}\) である。
原点における接空間 \({T_0\RR^n}\) の基底 \(e_1, \dotsc, e_{2m}\) に対する双対基底 \(e_1^*, \dotsc, e_{2m}^*\) を使って次のように書ける:
\[\omega(0) = e_1^* \wedge e_2^* + \dotsb + e_{2m - 1}^* \wedge e_{2m}^*.\]\({\omega^m \ne 0}\) である。
逆に
偶数次元ユークリッド空間の原点近傍で定義されている 2 形式 \(\omega\) が \({\omega^m \ne 0}\) であるならば、\({\omega(0)}\) は上の形に書ける。
まずベクトル場 \({\xi, \eta \in \mathfrak{X}(\RR^n)}\) に対する値 \({\omega(\xi, \eta)}\) を考える。
\({\omega(\xi, \eta) = -\omega(\eta, \xi)}\) が成り立つ(交代形式)。
\({\ker\omega = 0}\) より、これは非退化である。すなわち \({\xi \ne 0}\text{ or }{\eta \ne 0} \implies {\omega(\xi, \eta) \ne 0.}\)
原点における接空間 \({T_0\RR^n}\) の基底 \(\dfrac{\partial}{\partial x_i}\) をとって、各ベクトル場に成分表示を与えておく:
\[\begin{split}\begin{align*} \xi &= \sum_{i = 1}^n \xi_i \dfrac{\partial}{\partial x_i}\\ \eta &= \sum_{i = 1}^n \eta_i \dfrac{\partial}{\partial x_i} \end{align*}\end{split}\]まず 3. により \(\displaystyle {\omega(\xi, \eta) = \sum a_{ij}\xi_i\eta_j}\) の形に表せる。さらに 1. により \({a_{ij} = -a_{ji}}\) が成り立つ。
行列 \({A = (a_{ij})}\) とおく。これは実交代行列であるので線形代数論により、ある直交行列が存在して次の形の行列に対して共役となる:
\[\begin{split}\bigcup_k \begin{pmatrix} 0 & \lambda_k\\ -\lambda_k & 0 \end{pmatrix} \cup \begin{pmatrix} 0 & 0\\ 0 & 0 \end{pmatrix}\end{split}\]したがって対応する \({T_0\RR^n}\) の基底 \(e'_1, \dotsc, e'_n\) およびその双対基底 \({e_1^*}', \dotsc, {e_n^*}'\) がとれて次の形に書ける:
\[\omega = \lambda_1 {e_1^*}' \wedge {e_2^*}' + \dotsb + \lambda_m {e_{2m - 1}^*}' \wedge {e_{2m}^*}' \quad(2m \le n).\]本書では接空間の基底の外積の線形結合で書かれていたが、余接空間の基底に勝手に直しておく。
不等式は固有値の重複度を考慮したからか?
\({\ker\omega = 0}\) ゆえ 6. の式は \({2m = n}\) で成り立つ。
基底を調節して \(e_{2k - 1} = \dfrac{e'_{2k - 1}}{\lambda_{2k - 1}}, \ {e_{2k} = e'_{2k}}`と置き換え、:math:`e_i\) の双対基底を \(e_i^*\) と書けば、本問の冒頭の \({\omega(0)}\) に関する等式が成り立つことになる。
注意 4.3.13: 閉形式の場合
さらに \(\omega\) が閉形式であれば、後述する 問題 4.3.17 により空間各点の座標近傍で次の形のものがあることがわかる:
\[\omega = \dd x_1 \wedge \dd x_2 + \dotsb + \dd x_{2m - 1} \wedge \dd x_{2m}.\]
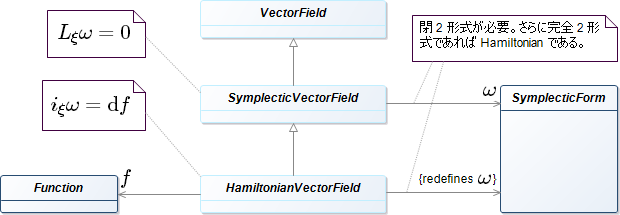
定義 4.3.14: シンプレクティク形式
\({\ker\omega = 0}\) をみたす \({\omega \in Z^2(M)}\) を シンプレクティク形式 という。
シンプレクティク多様体 とは、シンプレクティク形式を備えた多様体のことをいう。
例えば \({T_x^*M}\) は p. 156 で言及されているようにシンプレクティク多様体である。
ハミルトン関数
\(\RR^{2m}\) 上のシンプレクティク形式 \(\omega\) に対し、ベクトル場 \(\xi\) がそれを保つならば、命題 4.1.8 カルタンの公式と 定理 1.7.2 ポアンカレの補題により \({i_\xi\omega = \dd f}\) をみたす関数 \(f\) が存在する。この関数を ハミルトン関数 という。
もう少し用語を追加しておく。ベクトル場 \(\xi\) が シンプレクティクベクトル場 であるとは、シンプレクティク形式 \(\omega\) に対し次をみたすものをいう:
\[L_{\xi}\omega = 0.\]ベクトル場 \(\xi\) が生成するフローによって \(f\) は一定である。
なぜならば \({\xi(f) = (\dd f)(\xi) = i_\xi i_\xi \omega = 0.}\)
逆に \({\alpha \in Z^1(\RR^{2m})},\ {i_\xi\alpha = 0}\) なるベクトル場 \(\xi\) は一意的に定まる。この \(\xi\) が生成するフローは \(\omega\) を保つ。フローの軌道は葉層構造の葉の上にある。
ここで 定理 4.3.1 により \({\alpha \ne 0.}\)
-
シンプレクティク多様体 \(M\) 上の関数 \(f\) に対して次の式で定まるベクトル場 \(X_f\) を ハミルトン・ベクトル場 と呼ぶ:
\[i_{X_f}\omega = \dd f.\]ハミルトン・ベクトル場はシンプレクティクベクトル場である。
例えば 注意 4.3.13 のシンプレクティク形式に対する関数 \({f(x_1, \dotsc, x_{2m})}\) のハミルトン・ベクトル場はこうである:
\[\dfrac{\partial f}{\partial x_2}\dfrac{\partial}{\partial x_1} - \dfrac{\partial f}{\partial x_1}\dfrac{\partial}{\partial x_2} + \dotsb + \dfrac{\partial f}{\partial x_{2m}}\dfrac{\partial}{\partial x_{2m - 1}} - \dfrac{\partial f}{\partial x_{2m - 1}}\dfrac{\partial}{\partial x_{2m}}.\]
-
正確な定義は難しいので、雑バージョンを記す。シンプレクティック多様体 \((M, \omega)\) の部分多様体 \(L\) が ラグランジュ部分多様体 であるとは、次の条件を満たすはめ込みまたは埋め込み部分多様体のことである:
\({\forall x \in L,} {\forall v \in T_xM,} {\forall w \in T_xL,} {\omega(v, w) = 0.}\)
\({\dim L = \dim M / 2.}\)
余接束 には標準的シンプレクティク形式が定まる。
状況
多様体 \(M\) の次元を \(n\) とする。
ある点の座標近傍を \({(U, \varphi = (x_1, \dotsc, x_n))}\) とおく。
射影を \(\fn{p}{T^*M}M\) とおく。
写像 \(\fn{\widehat{\varphi}}{p\inv(U)}{\varphi(U) \times \RR^n}\) を定義する。ここで像の点 \({(x_1, \dotsc, x_n, y_1, \dotsc, y_n)}\) の後半部分は前半部分が表す点に対する接空間の双対ベクトルか。
ここで \({\theta = \sum_{i = 1}^n {y_i\,\dd x_i} \in \varOmega^1(T^*M)}\) とおく。
これは座標近傍の取り方に依存しない。
\(\displaystyle {\omega = -\dd \theta = \sum_{i = 1}^n \dd x_i \wedge \dd y_i}\) は余接束上のシンプレクティク形式になる。
リーマン多様体の余接束上には二次形式が定まる。
\[q^*\colon \sum_{i = 1}^n y_i\,\dd x_i \longmapsto \sum_{i,j = 1}^n g^{ij}y_i y_j.\]ここでリーマン計量を \(g_{ij}\) とし、その逆行列を \(g^{ij}\) とする。
問題 4.3.15: リーマン計量の二次形式が余接束に定めるハミルトン・ベクトル場
幾何学 I 7.2 や後述の節を参照。
Todo
これは後ほど取り組む。
問題 4.3.16: 全微分と余接束のシンプレクティク形式
\(M\) 上の関数 \(f\) の全微分は写像 \(\fn{\dd f}{M}T^*M\) とみなせる。
\({T^*M}\) のシンプレクティク形式 \(\omega\) に対して \({(\dd f)^*\omega = 0}\) が成り立つ。
全微分はこのような和である:
\[\dd f = \sum_{i = 1}^n \dfrac{\partial f}{\partial x_i}\,\dd x_i.\]先ほどの座標表記を用いると:
\[\dd f\colon (x_1, \dotsc, x_n) \longmapsto \left(x_1, \dotsc, x_n, \dfrac{\partial f}{\partial x_1}, \dotsc, \dfrac{\partial f}{\partial x_n}\right).\]引き戻しを計算する:
\[\begin{split}\begin{align*} (\dd f)^*\omega &= (\dd f)^*\left(\sum_{i = 1}^n \dd x_i \wedge \dd y_i\right)\\ &= \sum_{i = 1}^n \dd x_i \wedge \dd\left(\dfrac{\partial f}{\partial x_i}\right)\\ &= \sum_{i = 1}^n \dd x_i \wedge \sum_{j = 1}^n \dfrac{\partial^2 f}{\partial x_i}{\partial x_j}\,\dd x_j\\ &= \sum{1 \le i < j \le n}\dfrac{\partial^2 f}{\partial x_i}{\partial x_j}( \dd x_i \wedge \dd x_j + \dd x_j \wedge \dd x_i)\\ &= 0. \end{align*}\end{split}\]最初の等号は余接束の標準的シンプレクティク形式。
二番目の等号は 1. による。
三番目の等号は関数の全微分である。
四番目の等号は直接計算。ここは本書の解答例とみてくれが異なるが、意味は同じ。
最後の等号は外積の反対称性による。
定理 4.3.17: ダルブーの定理(シンプレクティク版)
\(2m\) 次元シンプレクティク多様体 \(M\) のシンプレクティク形式 \(\omega\) に対し、点 \({x^0 \in M}\) の座標近傍 \({(U, \varphi = (y_1, \dotsc, y_{2m}))}\) で次のように書けるものがある:
\[\omega = \dd y_1 \wedge \dd y_2 + \dotsb + \dd y_{2m - 1} \wedge \dd y_{2m}.\]局所標準形という座標近傍の存在定理である。
また、この座標を(座標成分の順序を変える必要があるかもしれないが)正準座標と呼ぶ。
以下証明。
色々なものを定義する:
開集合 \({U \subset M}\) を \(x^0\) の近傍とする。
関数 \(\fn{y_1}{U}\RR\) を \({(\dd y_1)_{(x^0)} \ne 0}\) となるように定める。
この関数についてのハミルトン・ベクトル場 \(X_{y_1}\) を定義する。すなわち \({i_{X_{y_1}}\omega = \dd y_1}\) が成り立つ。
およびこのベクトル場が生成する局所フローを \({\varphi_t^{(1)}(x)}\) とする。
このとき次の条件を満たす \({2m - 1}\) 次元部分多様体 \({D^{2m - 1} \subset M}\) が存在する:
\({x^0 \in D^{2m - 1}.}\)
\(X_{y_1}\) に横断的である。
なぜならば 1. より \({(\dd y_1)_{(x^0)} \ne 0} \implies {(X_{y_1})_{x^0} \ne 0}\) だからだ。
関数 \(\fn{y_2}{U}\RR\) を \({\varphi_{-y_2(x)}^{(1)} \in D^{2m - 1}}\) となるように定める。
\({y_1 = \text{const.}}\) および \({y_2 = \text{const.}}\) であるような二つの \({2m - 1}\) 次元部分多様体は \(x^0\) の近傍で横断的に交わる。
3. の関数に対応するハミルトン・ベクトル場を \(X_{y_2}\) とする。すなわち \({i_{X_{y_2}}\omega = \dd y_2}\) が成り立つ。さらにこのベクトル場が生成する局所フローを \({\varphi_t^{(2)}(x)}\) とする。このとき、
\({i_{X_{y_1}} i_{X_{y_2}} \omega = i{X_{y_1}}}\)
\({\dd y_2 = 1}\)
より \({i_{X_{y_2}} i_{X_{y_1}} \omega = i_{X_{y_2}}\,\dd y_1}\) が言えるから、フロー \(\varphi_t^{(2)}\) は
\({y_1 = -t}\) に写し、
\(X_{y_1}, X_{y_2}\) は可換
\[\begin{split}\begin{align*} i_{[X_{y_1}, X_{y_2}]}\omega &= (i_{X_{y_1}}L_{X_{y_2}} - L_{X_{y_2}}i_{X_{y_1}})\omega\\ &= i_{X_{y_1}}0 - L_{X_{y_2}}\,\dd y_1\\ &= -\dd i_{X_{y_2}}\,\dd y_1\\ &= -\dd(-1)\\ &= 0. \end{align*}\end{split}\]
である。よって二つのフロー \(\varphi_s^{(1)}, \varphi_t^{(2)}\) は可換である。
4. における二つの部分多様体の交差部分からなる部分多様体を \(B^{2m - 2}\) とおく。このとき、接空間 \(T_xB^{2m - 2}\) と \(T_xM\) の両方の部分空間 \({\langle X_{y_1}, X_{y_2} \rangle}\) は \(\omega\) に対して直交する。
なぜならば \({\forall v \in T_xB^{2m - 2}}\) に対して \(0 = {v(y_k)} = {i_v(\dd y_k)} = {i_v i_{X_{y_k}}\omega} \quad{(k = 1, 2)}\) だからだ。
ゆえに \({\ker(\omega|B^{2m - 2}) = 0.}\)
6. より \({\omega|B^{2m - 2} \in Z^2(B^{2m - 2})}\) はシンプレクティク形式である。
ここまでが証明の前半部分。残りは帰納法となる。
本定理の主張が \(2, 4, \dotsc, {2m - 2}\) 次元のシンプレクティク多様体に対して成り立っていると仮定する。このとき \(B^{2m - 2}\) 上の座標 \({(y_3, \dotsc, y_{2m})}\) で次のように表せるものが存在する:
\[\omega|B^{2m - 2} = \dd y_3 \wedge \dd y_4 + \dotsb + \dd y_{2m - 1} \wedge \dd y_{2m}.\]ここは複雑に見える。次の条件を満たす \({\eps \gt 0}\) が存在するということらしい:
\(\set{(\varphi_s^{(1)}(x), \varphi_t^{(2)}(x)) \sth s, t \in (-\eps, \eps)}\) と \({(-\eps, \eps) \times (-\eps, \eps)}\) は微分同相である。
二つのフローの可換性により、この各座標をフロー不変であるように \(x^0\) の近傍で定められる。このとき、ベクトル場 \(X_j\quad{(j = 3, \dotsc, 2m)}\) をハミルトン・ベクトル場として定める: \({i_{X_j}\omega = \dd y_j.}\)
ベクトル場 \(X_j, X_k\quad{(j, k = 3, \dotsc, 2m)}\) は可換である。
関数 \(y_1, y_2, y_3, \dotsc, y_{2m}\) を座標にとると、\(\omega\) は主張のように書かれる。
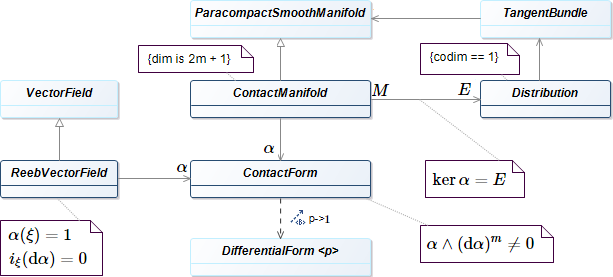
4.3.5 接触形式とレーブ・ベクトル場¶
奇数次元多様体 \(M^{2m + 1}\) 上の
値がゼロにならない \({\alpha \in \varOmega^1(M^{2m + 1})}\) は \(2m\) 次元の核を持つ。
\({\dd\alpha \in \varOmega^2(M^{2m + 1})}\) は次元が 1 以上の核を持つ。 定理 4.3.12 参照。
問題 4.3.18: 奇数次元空間で \({\ker(\dd\alpha)}\) \(\ker\alpha\) が横断的に交わる状況
\({\alpha \in \varOmega^1(\RR^{2m + 1})}\) が \({\ker(\dd\alpha) \cap \ker\alpha = 0}\) を満たすならば、原点における接空間の基底 \(e_0, e_1, \dotsc, e_{2m}\) で次を満たすものが存在する:
\[\alpha(0) = e_0,\quad \dd\alpha(0) = e_1 \wedge e_2 + \dotsb + e_{2m - 1} \wedge e_{2m}.\]また、\({\alpha \in \varOmega^1(\RR^{2m + 1})}\) が \({\alpha \wedge (\dd\alpha)^m \ne 0}\) であれば、\(\alpha(0)\) は上の形になる。
証明手順は 問題 4.3.12 と似ている。
横断的であることから \({\ker((\dd\alpha)|\ker\alpha) = 0.}\)
\(\ker\alpha(0)\) の基底 \(e'_1, \dotsc, e'_{2m}\) をとり、次のように表せる:
\[(\dd\alpha)|\ker\alpha = {e_1^*}' \wedge {e_2^*}' + \dotsb + {e_{2m - 1}^*}' \wedge {e_{2m}^*}'.\]\(\ker\alpha(0)\) 上の交代形式に対する基底とする。
\({\alpha(0)(e'_0) = 1}\) となるように \(e'_0\) を定め、接空間 \(T_0\RR^{2m + 1}\) の基底 \(e'_0, e'_1, \dotsc, e'_{2m}\) を得る。
3. の双対基底に対して次が成り立つような \(\set{a_i}\) が存在する:
\[\begin{split}\begin{align*} \alpha(0) &= {e_0^*}',\\ (\dd\alpha)(0) &= \sum_{i = 1}^{2m} a_i {e_0^*}' \wedge {e_i^*}' + {e_1^*}' \wedge {e_2^*}' + \dotsb + {e_{2m - 1}^*}' \wedge {e_{2m}^*}'. \end{align*}\end{split}\]接空間 \(T_0\RR^{2m + 1}\) の基底 \(e_0, e_1, \dotsc, e_{2m}\) を 4. を用いて次のようにして得る:
\[\begin{split}e_i = \begin{cases} \displaystyle \sum_{j = 1}^m(a_{2j}e_{2j - 1} - a_{2j - 1}e_{2j}) &\quad\text{if }i = 0,\\ e_i' & \quad\text{otherwise}. \end{cases}\end{split}\]そして 5. の双対基底を次のようにする:
\[\begin{split}\begin{align*} e_0^* &= {e_0^*}',\\ e_{2j - 1}^* &= {e_{2j - 1}^*}' + a_{2j}{e_0^*}',\\ e_{2j}^* &= {e_{2j}^*}' - a_{2j - 1}{e_0^*}'. \end{align*}\end{split}\]奇数項の外積を計算すると:
\[\begin{split}\begin{align*} e_{2j - 1}^* \wedge e_{2j}^* &= ({e_{2j - 1}^*}' + a_{2j}{e_0^*}') \wedge ({e_{2j}^*}' - a_{2j - 1}{e_0^*}')\\ &= {e_{2j - 1}^*}' \wedge {e_{2j}^*}' + a_{2j - 1}{e_0^*}' \wedge {e_{2j - 1}^*}' + a_{2j}{e_0^*}' \wedge {e_{2j}^*}'. \end{align*}\end{split}\]よって主張の等式の両方を得る。
ここから後半を証明する。
\({\alpha \wedge (\dd\alpha)^m \ne 0}\) であれば、\({\alpha \ne 0}\) かつ \({\ker((\dd\alpha)^m|\ker\alpha) = 0.}\)
\({\ker((\dd\alpha)|\ker\alpha) \subset \ker((\dd\alpha)^m|\ker\alpha)}\) であるから \(\ker((\dd\alpha)|\ker\alpha) = 0.\) あとは 1. 以降の議論に合流する。
注意 4.3.19: 実は 定理 4.3.24 ダルブーの定理によるとより強いことが言える。
定義 4.3.20: 接触形式
\({\alpha \in \varOmega^1(M)}\) が接触形式であるとは、\({\alpha \wedge (\dd\alpha)^m \ne 0}\) であって、値がゼロとならないものをいう。
定義 4.3.21: 接触構造・接触多様体
接触構造 とは、多様体 \(M\) 上の余次元 1 の平面場 \(E\) であって、各点の周りで \({E = \ker\alpha}\) が成り立つ \({\alpha \in \varOmega^1(M)}\) が接触形式であるものをいう。
多様体が 接触多様体 であるとは、それが接触構造を有することを意味する。接触多様体であることを強調するときは \({(M, E)}\) のように表記する。
問題 4.3.22: \({4m - 1}\) 次元接触多様体は向き付け可能
接触形式と非ゼロ関数をそれぞれ \(\alpha\) と \(g\) とおく。
体積形式 \({\alpha \wedge (\dd\alpha)^{2m - 1}}\) を意識して、 \(g\alpha\) の定める体積形式を計算する:
\[(g\alpha) \wedge (\dd(g\alpha))^{2m - 1} = g^{2m}\alpha \wedge (\dd\alpha)^{2m - 1}\]式変形において \({\dd(g\alpha) = \dd{g}\alpha + g\,\dd\alpha}\) を用いる。
1. により \({g^{2m} \gt 0}\) であるから多様体に対する向き付けは \(\alpha\) のとり方に依存しない。すなわち多様体が向き付け可能であることを意味する。
-
ベクトル場 \(\xi\) が レーブ・ベクトル場 であるとは、奇数次元多様体上の接触形式 \(\alpha\) に対して次を満たすベクトル場である:
\({\alpha(\xi) = 1}\)
\({i_\xi\dd\alpha = 0}\)
接触多様体の接触構造を保つ群は、多様体に推移的に作用する。
接触多様体 \({(M, E)}\) のはめ込みまたは埋め込み部分多様体 \(L\) がルジャンドル部分多様体であることは、各点 \({x \in L}\) で \({T_xL \in E}\) を満たすことと同値である。
問題 4.3.23: \(\CC^{n + 1}\) 上のシンプレクティク形式
\(\CC^{n + 1} = \set{\bm z = (z_1, \dotsc, z_{n + 1}) \sth z_1 \in \CC, \dotsc, z_{n + 1} \in \CC}\)
\(\displaystyle \omega = {\sum_{k = 1}^{n + 1}}\,{\dd x_k \wedge \dd y_k}\)
\({z_k = x_k + \sqrt{-1}y_k}\)
とおく。
(1) 関数 \(\displaystyle f(\bm z) = \frac{1}{2}\sum_{k = 1}^{n + 1}\abs{z_k}^2\) に対するハミルトン・ベクトル場 \(X_f\) は?
\({i_{X_f}\omega = \dd f}\) を満たすベクトル場 \(X_f\) を計算で求める。
直接計算により \({\dd f}\) を求める:
\[\dd f = -\sum_{k = 1}^{n + 1}(x_k,\dd x_k + y_k,\dd y_k).\]これが \(\displaystyle i_{X_f}\omega = i_{X_f}{\left(\sum_{k = 1}^{n + 1}\,\dd x_k \wedge \dd y_k\right)}\) と等しくなるようにベクトル場 \(X_f\) を決める。
定義 4.1.5 のとおりにやれば出てくるが、符号 \((-1)^{j - 1}\) に注意して計算ミスをしないようにすること。
\[X_f = \sum_{k = 1}^{n + 1}\left(x_k \frac{\partial}{\partial y_k} - y_k \frac{\partial}{\partial x_k} \right).\]
(2) ハミルトン・ベクトル場 \(X_f\) はリー群 \(U(1)\) の \(\CC^{n + 1}\) 上へ次の作用を生成する:
\[\mathrm{e}^{\sqrt{-1}\theta} \in U(1),\ \bm z \longmapsto \mathrm{e}^{\sqrt{-1}\theta}\bm z.\]ベクトル場が生成するフローを常微分方程式を解くことで求める。
\(X_f\) に対応する常微分方程式は次である:
\[\begin{split}\diff{}{t} \begin{pmatrix} x_k \\ y_k \end{pmatrix} = \begin{pmatrix} 0 & -1\\ 1 & 0 \end{pmatrix} \begin{pmatrix} x_k \\ y_k \end{pmatrix}.\end{split}\]
初期条件を \({(x_k, y_k)}\) とすると、1. の解は次のとおり:
\[\begin{split}\begin{pmatrix} \cos t & -\sin t\\ \sin t & \cos t \end{pmatrix} \begin{pmatrix} x_k \\ y_k \end{pmatrix}.\end{split}\]これを複素数で表現すると求めるフロー \(R_\theta\) は(パラメーターを \(\theta\) と書き換えて)次である:
\[R_\theta(\bm z) = \mathrm{e}^{\sqrt{-1}\theta}\bm z.\]
(3) 微分 1 形式 \({\alpha \in \varOmega^1(\RR^{2n + 1})}\) を次で定義する:
\[\alpha = \frac{1}{2}\sum_{k = 1}^{n + 1}(-y_k\,\dd x_k + x_k\,\dd y_k).\]このとき \(\alpha\) は \(U(1)\) の作用で不変である。
この問題は \({L_{X_f}\alpha = 0}\) を示せば十分。命題 4.1.8 カルタンの公式を用いる。
(4) \({S^{2n + 1} \in \CC^{n + 1}}\) を単位球面とする。
(4.1) \(U(1)\) 作用はこの球面上に自由に作用する。
\({\bm z \in \CC^{n + 1}\minuszero}\) に対して \({\mathrm{e}^{\sqrt{-1}\theta}\bm z = \bm z \implies \mathrm{e}^{\sqrt{-1}\theta} = 1}\) であるから OK である。
(4.2) \({\dd\alpha|S^{2n + 1} = \omega|S^{2n + 1}}\) に対して次が成り立つ:
\[i_{X_f}(\dd\alpha|S^{2n + 1}) = L_{X_f}(\dd\alpha|S^{2n + 1}) = 0.\]急所の一つは \({\dd f}\) が \(f\) の等位面である \(S^{2n + 1}\) 上でゼロであることだ。これは (3) の計算の一部による。それゆえ \({i_{X_f}(\dd\alpha|S^{2n + 1}) = 0.}\)
もう一つの急所は 注意 4.1.2 と 問題 4.1.4 の可換性にある:
\[\begin{split}\begin{align*} L_{X_f}(\dd\alpha|S^{2n + 1}) &= \dd L_{X_f}(\alpha|S^{2n + 1})\\ &= \dd((L_{X_f}\alpha)|S^{2n + 1})\\ &= 0. \end{align*}\end{split}\]
(4.3) \({\alpha|S^{2n + 1}}\) は接触形式である。
\({(\dd\alpha)^n}\) を計算する:
\[(\dd\alpha)^n = n!\sum_{k = 1}^{n + 1}\,\dd x_1 \wedge \dd y_1 \wedge \overset{(\text{pop }\dd x_k \wedge \dd y_k)}{\dotsb} \wedge \dd x_{n + 1} \wedge \dd y_{n + 1}.\]\({\alpha \wedge (\dd\alpha)^n}\) を計算する:
\[\begin{split}\begin{align*} \alpha \wedge (\dd\alpha)^n &= \frac{1}{2}\sum_{k = 1}^{n + 1}(-y_k,\dd x_k + x_k\,\dd y_k) \wedge (\dd\alpha)^n\\ &= \frac{n!}{2}\sum_{k = 1}^{n + 1}(-y_k,\dd x_1 \wedge \dd y_1 \wedge \overset{(\text{replace with }\dd x_k)}{\dotsb} \wedge \dd x_{n + 1} \wedge \dd y_{n + 1}\\ &\quad + x_k\,\dd x_1 \wedge \dd y_1 \wedge \overset{(\text{replace with }\dd y_k)}{\dotsb} \wedge \dd x_{n + 1} \wedge \dd y_{n + 1})\\ &= \frac{n!}{2}i_{\grad(f)}\,\dd x_1 \wedge \dd y_1 \wedge \dotsb \wedge \dd x_{n + 1} \wedge \dd y_{n + 1}. \end{align*}\end{split}\]ここで \({\grad(f) = -X_f}\) である。
\(\grad(f)\) は球面に直交するベクトル場であるから、この球面上では 2. の値はゼロではない。
(5) \({\CC P^n = S^{2n + 1}/U(1)}\) 上に定まる閉 2 形式 \({\omega_{\CC P^n}\in Z^2(\CC P^n)}\) について次が成り立つ:
\({\omega_{\CC P^n}^n \in \varOmega^{2n}(\CC P^n)}\)
\({\omega_{\CC P^n}^n(\cdot) \ne 0}\)
\(\beta = {\dd\alpha|S^{2n + 1}} = {\omega|S^{2n + 1} \in \varOmega^2(S^{2n + 1})}\) とおく。
(4) より \({i_{X_f}\,\dd\beta} = {L_{X_f},\dd\beta} = 0.\)
問題 4.2.6 より \({\omega_{\CC P^n} = \beta \in Z^2(\CC P^n).}\)
射影を \(p\) とすると、\({p^*(\omega_{\CC P^n}^n)} = {(\dd\alpha)^n}\) は \(\ker\alpha\) 上ではゼロではない。
ここがわかりにくかった。
\[i_{X_f}\alpha = \frac{1}{2}\sum_{k = 1}^{n + 1}(y_k^2 + x_k^2) = \frac{1}{2}\]であるので、接写像 \(\fn{p_*}{TS^{2n + 1}}T\CC P^n\) を \(\ker\alpha\) 上に制限すればこれは全射である。
以上で主張二点が示せた。
定理 4.3.24: ダルブーの定理
\(M^{2m + 1}\) を接触多様体、
\({\alpha \in \varOmega^1(M^{2m + 1})}\) を局所的な接触形式
とする。このとき \({x^0 \in M^{2m + 1}}\) の座標近傍 \({(U, \varphi=(x_0, \dotsc, x_{2m}))}\) で \(\alpha\) を次のように表せるものが存在する:
\[\alpha = \dd x_0 + x_2\,\dd x_2 + \dotsb + x_{2m - 1}\,\dd x_{2m}.\]証明のポイントはポアンカレの補題とダルブーの定理シンプレクティク版を利用することだ。
次の準備をする:
\({W = M^{2m + 1} \times \RR_+}\) とする。\({2m + 2}\) 次元多様体である。
\(\fn{p}{W}M\) を射影とする。
\({\beta = tp^*\alpha \in \varOmega^1(W),}\ {t \in \RR_+}\) とする。 \(t\) を座標と考える。
\({\dd\beta}\) が \(W\) 上のシンプレクティク形式である (\({\ker\dd\beta = 0}\)) ことを示す。
\[\begin{split}\begin{align*} (\dd\beta)^{m + 1} &= (\dd t \wedge p^*\alpha + tp^*\,\dd\alpha)^{m + 1}\\ &= (m + 1)t^m\,\dd t \wedge p^*\alpha \wedge (p^*\,\dd\alpha)^m + t(p^*\,\dd\alpha)^{m + 1}\\ &= (m + 1)t^m\,\dd t \wedge p^*\alpha \wedge (p^*\,\dd\alpha)^m + tp^*(\dd\alpha)^{m + 1}\\ &= (m + 1)t^m\,\dd t \wedge p^*(\alpha \wedge (\dd\alpha)^m)\\ &\ne 0. \end{align*}\end{split}\]三番目の等号は \({2m + 2}\) 形式の引き戻しを利用した。
シンプレクティク形式 \({\dd\beta}\) に 定理 4.3.17 ダルブーの定理シンプレクティク版を適用する。これにより \({(x^0, 1) \in W}\) の近傍で次のように表せる(次元に注意):
\[\dd\beta = \dd y_1 \wedge \dd y_2 + \dotsb + \dd y_{2m + 1} \wedge \dd y_{2m}.\]もう一つ 1 形式 \({\widehat\alpha = y_1\,\dd y_2 + \dotsb + y_{2m + 1}\,\dd y_{2m}}\) を考える。 \({\dd\widehat\alpha = \dd\beta}\) が成り立つ。そこで 定理 1.7.2 ポアンカレの補題を適用すると、次の条件を満たす関数 \(f\) が \({(x^0, 1)}\) の近傍で存在する:
\({\beta - \widehat\alpha = \dd f}\)
\({f(x^0, 1) = 0}\)
定理 4.3.17 における関数 \(y_1\) はゼロでさえなければよいので、\({y_1 = t}\) としてよい:
\[\beta = \widehat\alpha + \dd f = t\,\dd y_2 + \dd f + y_3\,\dd y_4 + \dotsb + y_{2m - 1}\,\dd y_{2m} + y_{2m + 1}\,\dd y_{2m + 2}.\]写像 \(\fnm{s}{M}{W}{x}{(x, 1)}\) を定義する。このとき次の等式が成り立つ:
\[\alpha = s^*\beta = \dd y_2 + \dd f + y_3\,\dd y_4 + \dotsb + y_{2m - 1}\,\dd y_{2m} + y_{2m + 1}\,\dd y_{2m + 2}.\]\({s^*(y_2 + f)}, {s^* y_3}, \dotsc, {s^* y_{2m + 2}}\) をそれぞれ \(x_0, x_1, \dotsc, x_{2m}\) とおいて座標関数とすれば、\(\alpha\) は主張の形となる。