102 日目(晴れ)記憶力劣化
0:00 フリーリを倒してから寝る。このゲームのラスボス戦からエピローグまでの流れがけっこう気に入っているので、何度もやってしまう。 それはさておき熱帯夜であるのか、部屋の暑さが執拗にあとを引く。眠れるのか、こんな条件で。
8:20 起床。すこぶるだるい。今日はノルマがないので気分は軽いのだが、肉体的には重たい。 とにかく朝飯にする。納豆とおにぎり。赤飯と野菜ジュースの相性が悪いというのを発見する。
9:00 PC 作業開始。きのうの確率統計の演習からやるか。もうボロボロ忘れている。 計算機的に浮動小数点の等間隔データを生成するのが難しいことを発見する。
正午前に PC をかばんに詰めて外出。三ツ目通りのバス停から金町駅行に乗る。 あっという間に四ツ木橋南詰に到着。日射に気をつけて八広図書館に移動。
朝刊を読んでキャレルに着席。月刊将棋世界を取ってくるが、結局ほとんど読まずにインターネットを調べる。 今日は地獄の伯爵令嬢の復習で使われている BGM さがし。ドキュメントに記載があるとおりに手に入る。
ビートマニアの新曲コメントを読めたので退館。別のバス通りに出る。
14:15 ビッグエー墨田八広店。210 円。
- コロッケドッグ
- コッペパンホイップ&チョコ
公園で食おうとしたらバス停にオッサンが複数つっ立っているので、先にバスを待つことにする。 錦糸町駅行きのバスが到着。乗り込む。暑いのでもう錦糸町駅まで行ってしまう。 ターミナルで降りてアルカキット錦糸町の日陰でパンを食らう。 エクセルシオールカフェの読みがわからないオバサンがスペリングを一文字ずつ大声で電話で伝えているのが面白い。
ハローワーク墨田に移動。検索して時間をつぶす。求人を見るのなら図書館でもできるのだが、そんなことに時間を使えない。
夕方、タイトー F ステーションオリナス錦糸町店に移動。 地下に降りる前にウォーターサーバーのセールスに捕まる。 ハローワーク帰りの人間にそんな上等なものを売りつけようとする心意気が気に入った。 もらったティッシュにある URL を貼っておくので、インターネットに接続できない私の代わりに誰か見ておいて欲しい。
気を取り直してゲーセンに入店。ビートマニアと MJ に 5 クレ使う。 ビートマニアは ARENA で韓国の猛者とマッチメイクしてしまう。 あまりの実力差に先方がレガシーオプションを付けるという配慮。それでも AA 行くのか。
麻雀はトップ 3 回二着 3 回を獲れてプレイ時間が押す。
【SCORE】
合計SCORE:+132.6
【最終段位】
四人打ち段位:雷神 幻球:10
【8/6の最新8試合の履歴】
1st|-*-**---
2nd|*-*---*-
3rd|--------
4th|-----*-*
old new
【順位】
1位回数:3(37.50%)
2位回数:3(37.50%)
3位回数:0(0.00%)
4位回数:2(25.00%)
平均順位:2.13
プレイ局数:42局
【打ち筋】
アガリ率:26.19%(11/42)
平均アガリ翻:3.73翻
平均アガリ巡目:10.73巡
振込み率:14.29%(6/42)
【8/6の最高役】
・跳満
・跳満
19:15 カスミオリナス錦糸町店。214 円。しらす丼。
19:40 ビッグエー墨田業平店。210 円。
- シュークリーム
- ふっくらおむすび各種 (2)
歩いて向島の部屋に戻る。おととい面接した会社から不採用通知が来ている。 シャワーを浴びてテレビを観ながら晩飯にする。しらす丼と冷奴の相性が良い。
PC をやる。数学の続きだ。積分の計算が一発で正解できてうれしい。 高校生の時ならこの程度は当たり前に出来ていたはずなのだがな。
23:00 全問片付ける。たぶん合っているだろう。
23:50 レベル 79 到達。次は 24 万。
Math Notes
薩摩順吉著『確率・統計』第 5 章演習問題に取り組む。
問:ボルト $40$ 本の標本を採り、長さを計測したら教科書のようなデータを得た。 ここから度数分布表とヒストグラムを作れ。それから標本平均をデータと表からそれぞれ計算しろ。 さらにこのデータから $5$ 本を無作為抽出して標本平均、標本分散を計算しろ。
解:Python ですべて計算する。
from statistics import fmean, variance
from random import sample
import numpy as np
import matplotlib.pyplot as plt
data = """
3.51
3.51
3.23
3.48
3.50
3.46
3.64
3.45
3.48
3.53
3.48
3.54
3.47
3.53
3.51
3.37
3.32
3.56
3.44
3.30
3.57
3.52
3.35
3.43
3.40
3.58
3.39
3.59
3.39
3.40
3.57
3.62
3.36
3.42
3.28
3.53
3.40
3.34
3.38
3.43
"""
SAMPLES = [float(i) for i in data.splitlines(False) if i]
def main():
#bin_numbers, bin_edges = np.histogram(SAMPLES, bins=np.linspace(3.2, 3.7, 6))
bin_numbers, bin_edges = np.histogram(SAMPLES, bins=(3.2, 3.3, 3.4, 3.5, 3.6, 3.7))
for i, j in zip(bin_numbers, bin_edges):
print(f'{j + .05:.02f} {i:>2}')
plt.figure()
plt.hist(SAMPLES, bins=bin_edges, histtype='stepfilled')
plt.show()
print(fmean(SAMPLES))
print(sum(i * (j + .05) for i, j in zip(bin_numbers, bin_edges)) / len(SAMPLES))
minisamples = sample(SAMPLES, 5)
minimean = fmean(minisamples)
print(f'Xbar = {minimean}')
print(f'S^2 = {variance(minisamples, minimean)}')
if __name__ == '__main__':
main()
実行結果:
3.25 2
3.35 9
3.45 13
3.55 14
3.65 2
3.4564999999999997
3.4625
Xbar = 3.5
S^2 = 0.024850000000000025
| 階級 | 個数 |
|---|---|
| 3.25 | 2 |
| 3.35 | 9 |
| 3.45 | 13 |
| 3.55 | 14 |
| 3.65 | 2 |
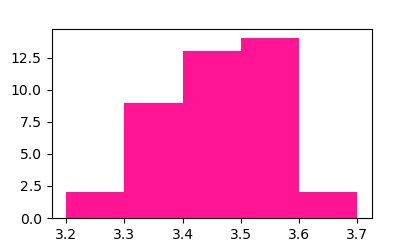
標本平均は直接計算すると $3.4565$ で代表値から計算すると $3.4625$ となる。
無作為抽出のものは実行するたびに結果が異なる。
問:$1$ から $99$ の数をランダムに出力し続ける装置がある。 この出力を母集団、出目を確率変数とする。
- 母平均、母分散を求めろ。
- $11, 22, …, 99$ が出る割合(母比率)はいくらか。
- $5$ 個出力して標本とし、標本平均 $\bar{X}$、標本分散 $S^2$ を計算することを繰り返す。 $\bar{X}$ の期待値、分散はいくらか。また $S^2$ の期待値はいくらか。
解:前半はとくに頭を使わない。
>>> from statistics import fmean, pvariance
>>> population = range(1, 100)
>>> mu = fmean(population); mu
50.0
>>> sigma2 = pvariance(population); sigma2
816.6666666666666
>>> 9 / len(population)
0.09090909090909091
Python によると $\mu = 50, \sigma^2 = 816.666…$ 指定の母比率は $9\%$ 程度。
後半は母平均、母分散との関係式を思い出す。
\[\begin{aligned} &E[\bar{X}] = \mu = 50,\\ &E[(\bar{X} - \mu)^2] = \dfrac{\sigma^2}{n} \approx 163.333,\\ &E[S^2] = \dfrac{n - 1}{n}\sigma^2 \approx 653.333. \end{aligned}\]>>> sigma2 / 5
163.33333333333331
>>> (5 - 1) / 5 * sigma2
653.3333333333334
問:ある養鶏場で生産する卵全体を母集団とする。 卵を $20$ 個無作為抽出すると、標本平均は平均と分散がそれぞれ $62.8, 5.2^2$ である分布に従うことがわかった。 母平均と母分散はいくらか。
解:母平均、母分散との関係により
\[\begin{aligned} \mu &= E[\bar{X}] = 62.8,\\ \sigma^2 &= nE[(\bar{X} - \mu)^2] = 20 \cdot 5.2^2 = 540.8 \approx 23.255^2. \quad\blacksquare \end{aligned}\]問:$1000$ 個すべての電気抵抗の値は平均が $100.2\Omega$ で標準偏差が $1.6\Omega$ である正規分布に従うことがわかっている。 今、ここから無作為に $5$ 個抽出して、その標本平均が $99\Omega$ から $101\Omega$ にある確率はいくらか。
解:母集団が $N(100.2, 1.6^2)$ に従うので、標本平均 $\bar{X}$ は $N(100.2, 1.6^2/5)$ に従う。
\[Z \coloneqq \frac{X - 100.2}{1.6 / \sqrt{5}}\]と変数変換すれば $Z$ は $N(0, 1)$ に従う。あとは計算機に任せる:
>>> from math import sqrt
>>> from scipy.stats import norm
>>> z1 = (99 - 100.2)/(1.6 / sqrt(5)); z1
-1.6770509831248461
>>> z2 = (101 - 100.2)/(1.6 / sqrt(5)); z2
1.118033988749891
>>> norm.cdf(z2) - norm.cdf(z1)
0.8214575050139666
もちろん norm.cdf(z, 100.2, 1.6 / sqrt(5)) のような計算コードも許される。
$\blacksquare$
問:一袋平均 $32$ 片入っているポテチがある。この商品を $25$ 品調べると標本平均と標本分散がそれぞれ $29.2, 5.5$ であった。このようなことは $100$ 回に一度も起こると言えるか。
解:次の $Z$ が $N(0, 1)$ に従う:
\[\begin{aligned} Z = \frac{\bar{X} - \mu}{S/\sqrt{n - 1}} = \frac{29.2 - 32}{5.5/\sqrt{24}}. \end{aligned}\]>>> Z = (29.2 - 32)/(5.5/sqrt(24)); Z
-2.494025919924691
>>> norm.cdf(Z)
0.0063151660474310535
$1/100 = 0.01$ より小さいので起こらないと言える。 $\blacksquare$
問:ここにある無数のビー玉の性質(質量か大きさか忘れた)は正規分布 $N(1.2, 0.3^2)$ に従う。 ここから $4$ 個を無作為に抽出して標本平均を計算すると値が $1.5$ 以上である確率はいくらか。
解:$Z = (\bar{X} - \mu)/(\sigma/\sqrt{n})$ が $N(0, 1)$ に従う。
\[\begin{aligned} \bar{X} &= \mu + \frac{\sigma}{\sqrt{n}}Z \ge 1.5\\ Z &\ge \frac{\sqrt{n}}{\sigma}(1.5 - \mu).\\ \therefore P(\bar{X}\!\ge\!1.5) &= P\!\left(Z\!\ge\!\frac{\sqrt{n}}{\sigma}(1.5 - \mu)\right)\\ &= P(Z \ge 2). \end{aligned}\]正規分布におけるこの手の値は憶えておいて損はないのだが:
>>> norm.sf(2)
0.022750131948179195
よって約 $2.3\%$ 。 $\blacksquare$
問:自由度 $4$ の $\chi^2$ 分布 $T_4(z)$ の値が最大となる $z = z0$ はいくらか。 また $P(z \ge z_0)$ の値はいくらか。
解:微分積分の問題。$z \ge 0$ を仮定してよい。
\[\begin{aligned} T_4(z) &= \frac{1}{2^{4/2}\varGamma(4/2)}z^{(4 - 2)/2}\mathrm{e}^{-z/2}\\ &= \frac{1}{4}z\mathrm{e}^{-z/2}.\\ \frac{\mathrm{d}T_4(z)}{\mathrm{d}z} &= \frac{1}{8}\left(2 - z\right)\mathrm{e}^{-z/2}. \end{aligned}\]$z = 2$ のとき極大値をとるので $z_0 = 2.$
後半は次の広義積分を計算する:
\[\begin{aligned} \int_2^\infty\!T_4(z)\,\mathrm dz &= \frac{1}{4}\int_2^\infty\!z\mathrm{e}^{-z/2}\,\mathrm dz\\ &= -\frac{1}{2}\left[z\mathrm{e}^{-z/2}\right]_2^\infty + \frac{1}{2}\int_2^\infty\!\mathrm{e}^{-z/2}\,\mathrm dz\\ &= -\frac{1}{2}(0 - 2\mathrm{e}^{-1}) - \left[\mathrm{e}^{-z/2}\right]_2^\infty\\ &= \frac{1}{\mathrm{e}} - (0 - \frac{1}{\mathrm{e}})\\ &= \frac{2}{\mathrm{e}}. \end{aligned}\]念のため:
>>> from scipy.stats import chi2
>>> n, z0 = 4, 2
>>> chi2(n).sf(z0)
0.7357588823428847
>>> from scipy import exp
>>> 2/exp(1)
0.7357588823428847
問:母平均が $-2.6$ の正規母集団から $8$ 個無作為抽出して標本を作り、 その標本平均と標本分散を計算したところ $-2.3, 0.16$ であった。 このような結果が生じる確率を $5\%$ と比較しろ。
解:$F$ 分布を応用する。
\[\begin{aligned} X &= \frac{(n - 1)(\bar{X} - \mu)^2}{S^2}\\ &= \frac{(8 - 1)(-2.3 + 2.6)^2}{0.16} = 3.9375. \end{aligned}\]>>> X = (8 - 1) * (-2.3 + 2.6)**2 / 0.16; X
3.937500000000007
>>> from scipy.stats import f
>>> f(1, 8 - 1).isf(0.05)
5.591447851220738
$3.9375 \lt 5.5914…$ だから $1\%$ より大きいと言える。 $\blacksquare$
問:自由度 $(2, 2)$ の $F$ 分布 $f_{2, 2}(x)$ を simplify しろ。 次に $\displaystyle \int_t^\infty f_{2, 2}(x)\,\mathrm dx = \alpha$ となる $t$ と $\alpha$ の関係式を積分を含まない形で表わせ。
解:
\[\begin{aligned} f_{2, 2}(x) &= \frac{2^{2/2}2^{2/2}x^{(2 - 2)/2}}{B(2/2, 2/2)(2x + 2)^{(2 + 2)/2}}\\ &= \frac{1}{B(1, 1)(x + 1)^2}\\ &= \frac{1}{(x + 1)^2}. \end{aligned}\] \[\begin{aligned} \int_t^\infty\!f_{2, 2}(x)\,\mathrm dx &= \int_t^\infty\!\frac{\mathrm dx}{(x + 1)^2}\\ &= -\left[\frac{1}{x + 1}\right]_t^\infty = \frac{1}{t + 1}.\\ \therefore \frac{1}{t + 1} &= \alpha. \quad\blacksquare \end{aligned}\]問:自由度 $1$ の $t$ 分布 $f_1(t)$ を simplify しろ。そしてその cdf が $1$ となることを示せ。
解:
\[\begin{aligned} f_1(t) &= \frac{1}{\sqrt{1}B(1/2, 1/2)(1 + t^2)^{(1 + 1)/ 2}}\\ &= \frac{\Gamma(1)}{\Gamma(1/2)\Gamma(1/2)(1 + t^2)}\\ &= \frac{1}{\pi(1 + t^2)}. \end{aligned}\]なお $\arctan$ を知らなくても次の広義積分は計算できるとのこと:
\[\begin{aligned} \int_{-\infty}^\infty\!f_1(t)\,\mathrm dt &= \frac{1}{\pi}\int_{-\infty}^\infty\!\frac{\mathrm dt}{1 + t^2}\\ &= \frac{1}{\pi}\bigg[\arctan t \bigg]_{-\infty}^\infty\\ &= \frac{1}{\pi}\!\left(\frac{\pi}{2} - \left(-\frac{\pi}{2}\right)\right)\\ &= 1. \quad\blacksquare \end{aligned}\]以上