124 日目(晴れ)業者からの連絡が来ない
9:00 過ぎにいつものようにいやいや起きる。朝飯。10:00 前に外出。
福祉事務所に行き、生活保護受給者証明書を一枚確保する。 きのうの契約は不成立に終わったことも報告する。
スカイツリータウンの書店で雑誌チェックをしてから押上駅周辺の不動産屋まわりを行う。 四ツ目通りの東側の店舗を片っ端から当たるが、だいたい門前払い。 そのうち長く話をしてくれた店があって、そこでコツのようなものを聞く。
ヤケを起こして横川コミュニティー会館図書室に移動。朝刊などを読む。
13:25 ビッグエー墨田業平店。166 円。
- 大きなおむすび鮭
- ジャムパン
押上駅バスターミナルのビル影で立ち食い。気を取り直して次の店へ行く。 もう西日がキツイので、東側に面した店舗からさがす。
この店は話がすんなり進み、私の条件で物件をいくつか探しておくから明日午後来いとのことになる。 今から大家に交渉しながら探すので時間がかかるのだ。
というわけで部屋探しは中断して錦糸町駅へ移動する。ハローワーク墨田で休憩をしてから(ここでしか水が飲めない)アルカキット錦糸町のくまざわ書店へ。 正直暑くて記憶が不確か。このあとオリナスへ移動したはず。噴水前で休憩か。
ヤマダ電機のテレビ売り場で首相の辞任演説を見る。16:30 頃にタイトー F ステーションオリナス錦糸町店に移動。 ビートマニアと MJ とで 5 クレ遊ぶ。
【SCORE】
合計SCORE:+4.2
【最終段位】
四人打ち段位:雷神 幻球:6
【8/28の最新8試合の履歴】
1st|------*-
2nd|---*-*--
3rd|--*-*--*
4th|--------
old new
【順位】
1位回数:1(16.67%)
2位回数:2(33.33%)
3位回数:3(50.00%)
4位回数:0(0.00%)
平均順位:2.33
プレイ局数:25局
【打ち筋】
アガリ率:8.00%(2/25)
平均アガリ翻:3.50翻
平均アガリ巡目:7.50巡
振込み率:4.00%(1/25)
【8/28の最高役】
最高役のデータがありません。最高役は、跳満以上のアガリが対象となります。
18:50 カスミオリナス錦糸町店。336 円。八宝菜&肉団子丼。
19:15 ビッグエー墨田業平店。284 円。
- シュークリーム
- 大きなおむすび鮭
向島の部屋に戻る。テレビを見ながら晩飯。そして PC を持って外出。 隅田公園トイレ経由で電話ボックスへ。メールチェックはやはりこちらのほうが安心だ。 GitHub にプッシュしている当ブログのビルドエラーくらいで、大したメールはない。 髭アーカイブの持っていない回のダウンロードをして終わる。
シャワーを浴びて PC 作業。汗が全然引かない。 ホームレス最終盤に悪化した股のまわりの湿疹だかなんだかはいつ治るのだろう。
21:55 数学ノートをやる。髭アーカイブの DUE TOMORROW 回はすごい。ロングになってさらに凶悪に。 髭先生のコメントも無責任で面白い。
22:40 地獄の昨日の続き。レイコ戦。タイマンでのダメージが思いの外大きくて終了。総プレイ時間不明。 またゼロからやリなおす。
タイタニア戦で死亡。もうダメだ。
Math Notes
薩摩順吉著『確率・統計』第 6 章末問題を解く。
問:新入生 $97$ 人の血液型を調べたところ、A 型が $51$ 人、O 型が $23$ 人、B 型が $14$ 人、AB 型が $9$ 人であった。 日本人の血液型の人口比は $38 : 31 : 22 : 9$ である。 新入生の血液型の人口比は母集団と合っているかどうか、危険率 $5\%$ で検定しろ。
解:帰無仮説 $H_0$ を「比率は合っている」とおく。なぜか片側検定。
まず期待度数を計算する。
>>> P = [38, 31, 22, 9]
>>> p = [i/sum(P) for i in P]; p
[0.38, 0.31, 0.22, 0.09]
>>> E = [i * 97 for i in p]; E
[36.86, 30.07, 21.34, 8.73]
期待度数と観測度数から $X$ を計算:
>>> O = [51, 23, 14, 9]
>>> X = sum((o - e)**2 / e for o, e in zip(O, E)); X
9.619562329047215
自由度 ${4 - 1 = 3}$ の $\chi^2$ 分布に従うので、
>>> chi2(4 - 1).isf(0.05)
7.814727903251178
$X = 9.619… \gt 7.81…$ であるから $X$ は棄却域にある。 したがって $H_0$ は棄却されて、比率に合っていないと言える。 $\blacksquare$
問:歌謡曲 $447$ 曲の題名とヒットしたかどうかを調べたところ次のようになった: 題名にカタカナが入っている・いないとヒットする・しないが関係しているかを危険率 $1\%$ で検定しろ。
| カタカナあり | カタカナなし | 計 | |
|---|---|---|---|
| ヒットした | 76 | 101 | 177 |
| ヒットしなかった | 31 | 239 | 270 |
| 107 | 240 | 447 |
解:喫煙の例題と同じ流れ。$H_0$ を「関係がない」とおく。 $X$ は自由度 $(2 - 1)(2 - 1)$ の $\chi^2$ 分布に従う。
>>> x = [[76, 31], [101, 239]]
>>> a = [107, 340]
>>> b = [177, 270]
>>> N = 447
>>> X = sum((x[i][j] - a[i] * b[j] / N)**2/(a[i] * b[j] / N) for i in range(2) for j in range(2)); X
58.103074406065296
>>> chi2(1).isf(0.01)
6.634896601021217
$X \gt 6.6348…$ だから棄却域にある。つまり関係があるといえる。 $\blacksquare$
問:$10$ 人集めて体重 $X$ とウエスト $Y$ を表にまとめた:
\[\begin{array}{r|} X & 53 & 47 & 55 & 56 & 55 & 54 & 54 & 55 & 53 & 56\\ Y & 56 & 52 & 64 & 60 & 56 & 57 & 58 & 57 & 58 & 57\\ \end{array}\]- 相関図を描け。$y = a + bx$ の回帰係数を求めろ。
- 標本相関係数、直線の誤差を求めろ。
- この標本は二次元正規分布から抽出されたものとみなせる。体重とウエストの間には相関関係があるかどうかを危険率 $5\%$ で検定しろ。
解:プロットは適当にやる。
>>> import numpy as np
>>> x = np.array([53, 47, 55, 56, 55, 54, 54, 55, 53, 56])
>>> y = np.array([56, 52, 64, 60, 56, 57, 58, 57, 58, 57])
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 1)
>>> ax.scatter(x, y)
<matplotlib.collections.PathCollection at 0x2182735e2e0>
>>> plt.show()
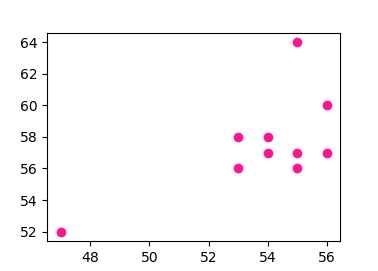
まず標本平均と標本分散を計算する。
>>> xbar = x.mean(); xbar
53.8
>>> sx2 = x.var()
6.159999999999998
>>> ybar = y.mean(); ybar
57.5
>>> sy2 = y.var(); sy2
8.45
標本共分散 $s_{xy}$ を計算する:
>>> sxy = sum(x * y)/x.size - xbar * ybar
4.800000000000182
これでようやく回帰係数 $a, b$ が得られる:
>>> a = ybar - sxy * xbar / sx2; a
15.57792207792049
>>> b = sxy / sx2; b
0.7792207792208087
標本相関係数 $C_{xy}$ は:
>>> Cxy = sxy/sqrt(sx2 * sy2); Cxy
0.6653076647598226
直線の誤差 $s_e^2$ は
\[s_e^2 = s_y^2(1 - C_{xy}^2).\]を使って求める:
>>> se2 = sy2 * (1 - Cxy**2); se2
4.709740259739976
検定は次のようにする。$H_0$ を「${\rho_{xy} = 0}$」とおく。両側検定。
>>> n = 10
>>> T = sqrt((n - 2) * Cxy**2 / (1 - Cxy**2)); T
2.5205620692429735
>>> t(n - 2).interval(1 - 0.05)
(-2.3060041350333704, 2.3060041350333704)
$T \gt 2.306…$ であるから棄却域にある。したがって $H_0$ は棄却される。 相関係数はゼロであるとは言えない:相関関係がある。 $\blacksquare$
以上