125 日目(晴れ)いいことがない日が驚くほど続く
午後が体力勝負になりそうなので長めに睡眠をとる。10:00 に起き上がる。 ねこの足跡&看板ねこを観ながら朝食。メールを確認したが、きのう訪問した業者からの連絡がない。 これは午後直接店舗に行っていいのか。
外出までダラダラ。10:45 外出。スカイツリータウンで時間つぶし。
13:00 昨日世話になった不動産仲介業者店舗を再訪問。話がちょっと違っていて、まだ物件を探してくれていないとのこと。 時間がかかるので見つかったらメールをくれるように依頼して去る。
横川コミュニティー会館図書室。朝刊と教科書を読む。東京新聞の安倍首相追及記事がエンジン全開。
15:15 ビッグエー墨田業平店まで戻って買い物。144 円。
- スナックサンドハムタマ
- パンケーキメープル&マー
横川五丁目団地地帯の木陰ベンチで食う。この暑いときにタバコを吸いに爺さんが来るのには驚いた。
タイトー F ステーションオリナス錦糸町店。週末なので混んでいる。MJ に絞る。 座ってからしばらくは好調だったのに、なぜか不運に見舞われまくって凡庸な成績で終わる。
【SCORE】
合計SCORE:-1.5
【最終段位】
四人打ち段位:雷神 幻球:11
【8/29の最新8試合の履歴】
1st|*-*-----
2nd|-*------
3rd|-----***
4th|---**---
old new
【順位】
1位回数:3(25.00%)
2位回数:3(25.00%)
3位回数:4(33.33%)
4位回数:2(16.67%)
平均順位:2.42
プレイ局数:59局
【打ち筋】
アガリ率:20.34%(12/59)
平均アガリ翻:2.67翻
平均アガリ巡目:11.67巡
振込み率:13.56%(8/59)
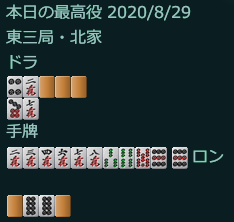
【8/29の最高役】
・倍満
19:05 カスミオリナス錦糸町店。247 円。四川風麻婆豆腐丼。
19:35 ビッグエー墨田業平店。159 円。
- シュークリーム
- 大きなおむすびツナマヨ
いつものようにスカイツリーギャラリー経由で向島の部屋に戻る。シャワーを浴びて晩飯。 麻婆豆腐が味が濃くて頭にガツンと来る。 ブラタモリとかカネオくんとかを観る。タモリが長崎の暗渠に潜るのには笑った。
21:05 数学ノート終わり。今日は何もない。テザリングで Twitter をチェック。 最古フォロワーサン、長らくのご愛顧誠にありがとうございました。
少し前にダウンロードしておいた都営バスの路線図 PDF を眺める。 新しい住所がどこになるかわからないが、都バスが近くにないところを今のうち覚えておかないとまずい。
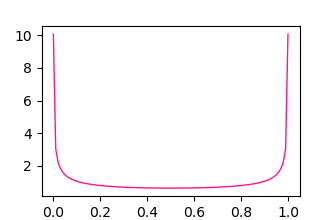
22:45 下のプロットを作図する。ランダムウォークは時間が経つと原点に入る確率がいちばん低い。 これは覚えておく。
残り時間は髭アーカイブ、麻雀の練習、ランちゃん。それにしても暑い。
Math Notes
薩摩順吉著『確率・統計』第 7 章。
確率過程。時刻 $t$ とともに変化する確率変数 $X(t)$ を確率過程とか時系列とかと呼ぶ。
$X(t)$ のとり得る値 $x(t)$ を $X(t)$ の標本関数という。 ${{X(t)} }$ のように集合の形式で表すことがある。
サイコロを時刻 $t$ で一個振って 1 の目が出た合計回数 $X(t)$ は例えば $t = 3$ では:
\[\begin{aligned} X(3) = \{ &\{(1, 0), (2, 0), (3, 0)\},\\ &\{(1, 0), (2, 0), (3, 1)\},\\ &\dotsc,\\ &\{(1, 1), (2, 2), (3, 3)\}\}. \end{aligned}\]確率分布は二項分布 ${\operatorname{Bin}(n, 1/6)}$。
\[f(x(n)) = \binom{n}{x}\left(\frac{1}{6}\right)^x \left(\frac{5}{6}\right)^{n - x}.\]例:時刻 $t$ にコイントスをして表が出れば ${X(t) = \sin t}$ とし裏が出れば ${X(t) = \cos t}$ で定義すると ${{X(t)} }$ は連続的な $t$ に対して定義される。
ランダムウォークは確率過程の一種である。
例:ある人が時刻 $t = 0$ で座標軸の原点にいる。 単位時間が経過すると確率 $p$ で ${+1}$ に、${1 - p}$ で ${-1}$ だけ移動する。 ${X(t)}$ をこの人の時刻 $t$ における位置で定義すると、${{X(t)} }$ は確率過程である。
${p = 1/2}$ とする。時刻 ${t = n}$ にこの人が位置 ${n - 2k\ (k \in \N)}$ にいる確率は
\[f(x(n)) = \binom{n}{k}\left(\frac{1}{2}\right)^k \left(\frac{1}{2}\right)^{n - k} = \binom{n}{k}\left(\frac{1}{2}\right)^n.\]$x(3)$ が ${3 - 2 \cdot 2 = -1}$ にいる確率は $3/8$ と計算できる。
ランダムウォークでは $0$ の周りをうろつくよりも、一方に偏ることが多い。 左右へ進む確率が同じランダムウォークにおいて、ある時間の間に原点の右側にいる確率を $a$ としたときの分布 $f(a)$ は次のようなものである(証明なし):
\[f(a) = \frac{1}{\pi \sqrt{a(1 - a)} }.\]import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1)
x = np.linspace(0.001, 0.999, 100)
y = 1 / (np.pi * np.sqrt(x * (1 - x)))
ax.plot(x, y)
plt.show()
拡散。中心極限定理により、十分時間が経ったときの無数のランダムウォーカーの分布は正規分布に従う。
二項分布 $\operatorname{Bin}(n, 1/2)$ において $n \to \infty$ のときの極限となる正規分布は、 平均、分散がそれぞれ ${\mu = n/2, \sigma^2 = n/4}$ である。 ここで ${z \coloneqq (k - \mu)/\sigma}$ とおくと分布関数は
\[f(z) = \frac{1}{\sqrt{2\pi} }\exp\!\left(-\frac{z^2}{2}\right)\]である。
${z = -\dfrac{1}{\sqrt{n} }(n - 2k)}$ をプロットすると、ランダムウォークが拡散現象の簡単なモデルであることが実感できる。
ランダムウォークは差分方程式で表せる。 ${P(m, n) \coloneqq P(x = m \land t = n)}$ と表し、左へ進む確率を $p,$ 右へ進む確率を $1 - p = q$ とおくと
\[P(m, n) = pP(m + 1, n - 1) + qP(m - 1, n - 1).\]${P(0, 0) = 1, P(m, 0) = 0\ (m \ne 0)}$ を順次解けば $f(x(n))$ を記述することができる。
簡単なケースを試す。${P(1, 1)}$ と ${P(-1, 1)}$ はそれぞれ右へ進む確率、左へ進む確率そのもののはずだ。
\[\begin{aligned} P(1, 1) &= pP(1 + 1, 1 - 1) + qP(1 - 1, 1 - 1)\\ &= pP(2, 0) + qP(0, 0)\\ &= p \cdot 0 + q \cdot 1\\ &= q.\\ P(-1, 1) &= pP(-1 + 1, 1 - 1) + qP(-1 - 1, 1 - 1)\\ &= pP(0, 0) + qP(-2, 0)\\ &= p \cdot 1 + q \cdot 0\\ &= p. \end{aligned}\]以上